Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T18:43:39.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Intersecting Families are Essentially Contained in Juntas

Published online by Cambridge University Press:  01 March 2009

IRIT DINUR  and
EHUD FRIEDGUT
IRIT DINUR
Affiliation:
School of Computer Science and Engineering, Hebrew University, Jerusalem, Israel (e-mail: [email protected])
EHUD FRIEDGUT
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem, Israel (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

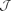A family of subsets of {1, . . ., n} is called a j-junta if there exists J ⊆ {1, . . ., n}, with |J| = j, such that the membership of a set S in 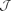depends only on S ∩ J.

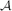In this paper we provide a simple description of intersecting families of sets. Let n and k be positive integers with k < n/2, and let be a family of pairwise intersecting subsets of {1, . . ., n}, all of size k. We show that such a family is essentially contained in a j-junta 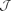, where j does not depend on n but only on the ratio k/n and on the interpretation of ‘essentially’.

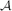When k = o(n) we prove that every intersecting family of k-sets is almost contained in a dictatorship, a 1-junta (which by the Erdős–Ko–Rado theorem is a maximal intersecting family): for any such intersecting family there exists an element i ∈ {1, . . ., n} such that the number of sets in 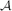that do not contain i is of order 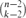(which is approximately 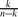times the size of a maximal intersecting family).

Our methods combine traditional combinatorics with results stemming from the theory of Boolean functions and discrete Fourier analysis.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 1-2: Papers from The 2006 Oberwolfach Meeting on Combinatorics, Probability and Computing , March 2009 , pp. 107 - 122
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ahlswede, R. and Khachatrian, L. (1997) The complete intersection theorem for systems of finite sets. Europ. J. Combin. 18 125–136.CrossRefGoogle Scholar
[2]Dinur, I., Friedgut, E. and Regev, O. Independent sets in graph powers are almost contained in juntas. To appear in G.A.F.A.Google Scholar
[3]Dinur, I. and Safra, S. (2005) On the hardness of approximating minimum vertex cover. Ann. of Math. 162 439–485.CrossRefGoogle Scholar
[4]Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. Oxford Ser. 2 12 313–318.CrossRefGoogle Scholar
[5]Frankl, P. and Tokushige, N. (1998) Some inequalities concerning cross-intersecting families. Combin. Probab. Comput. 7 247–260.CrossRefGoogle Scholar
[6]Friedgut, E. (1998) Boolean functions with low average sensitivity depend on few coordinates. Combinatorica 18 27–35.CrossRefGoogle Scholar
[7]Füredi, Z. (1995) Cross-intersecting families of finite sets. J. Combin. Theory Ser. A 72 332–339.CrossRefGoogle Scholar
[8]Katona, G. O. H. (1968) A theorem of finite sets. In Theory of Graphs (Erdőos, P. and Katona, G., eds), Akadémiai Kiadó and Academic Press, pp. 187–207.Google Scholar
[9]Kruskal, J. (1963) The number of simplices in a complex. In Mathematical Optimization Techniques (Bellman, R., ed.), University of California Press, pp. 251–278.CrossRefGoogle Scholar
[10]Margulis, G. (1974) Probabilistic characteristics of graphs with large connectivity. Prob. Peredachi Inform. 10 101–108.Google Scholar
[11]Mossel, E., O'Donnell, R. and Oleszkiewicz, K. (2005) Noise stability of functions with low influences: Invariance and optimality. In Proc. 46th IEEE Symp. on Foundations of Computer Science, pp. 21–30.CrossRefGoogle Scholar
[12]Russo, L. (1982) An approximate zero-one law. Z. Wahrsch. werw. Gebiete 61 129–139.CrossRefGoogle Scholar
[13]Tuza, Z. (1985) Critical hypergraphs and intersecting set-pair systems. J. Combin. Theory Ser. B 39 134–145.CrossRefGoogle Scholar