Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-20T11:42:01.939Z Has data issue: false hasContentIssue false
  • English
  • Français

The First k-Regular Subgraph is Large

Published online by Cambridge University Press:  07 April 2014

PU GAO
PU GAO*
Affiliation:
Department of Computer Science, University of Toronto10 King's College Road, Toronto, ON M5S 3G4, Canada (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 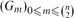$(G_m)_{0\le m\le \binom{n}{2}}$ be the random graph process starting from the empty graph on vertex set [n] and with a random edge added in each step. Let mk denote the minimum integer such that Gmk contains a k-regular subgraph. We prove that for all sufficiently large k, there exist two constants εk ≥ σk > 0, with εk → 0 as k → ∞, such that asymptotically almost surely any k-regular subgraph of Gmk has size between (1 − εk)|${\mathcal C}_k$| and (1 − σk)|${\mathcal C}_k$|, where ${\mathcal C}_k$ denotes the k-core of Gmk.

Keywords

05C80
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 3 , May 2014 , pp. 412 - 433
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bollobás, B. (2001) Random Graphs, second edition, Vol. 73 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.Google Scholar
[2]Bollobás, B., Kim, J. and Verstraëte, J. (2006) Regular subgraphs of random graphs. Random Struct. Alg. 29 1–13.Google Scholar
[3]Cain, J. and Wormald, N. (2006) Encores on cores. Electron. J. Combin. 13 R81.Google Scholar
[4]Chan, S. and Molloy, M. (2012) (k + 1)-cores have k-factors. Combin. Probab. Comput. 21 882–896.Google Scholar
[5]Erdős, P. and Rényi, A. (1961) On the evolution of random graphs. Bull. Inst. Internat. Statist. 38 343–347.Google Scholar
[6]Gao, P. and Wormald, (2010) Load balancing and orientabililty thresholds for random hypergraphs, In Proceedings of the 42nd ACM Symposium on Theory of Computing, 5–8 June, Cambridge, MA, USA.Google Scholar
[7]Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience.CrossRefGoogle Scholar
[8]Letzter, S. (2013) The property of having a k-regular subgraph has a sharp threshold. Random Struct. Alg. 42 509–519.Google Scholar
[9]McKay, B. D. (1985) Asymptotics for symmetric 0–1 matrices with prescribed row sums. Ars Combinatoria 19A 15–25.Google Scholar
[10]McKay, B. D. and Wormald, N. C. (1990) Asymptotic enumeration by degree sequence of graphs of high degree. Europ. J. Combin. 11 565–580.Google Scholar
[11]McKay, B. D. and Wormald, N. C. (1991) Asymptotic enumeration by degree sequence of graphs with degrees $o(\sqrt{n})$. Combinatorica 11 369–382.CrossRefGoogle Scholar
[12]Pittel, B. and Spencer, J. and Wormald, N. (1996) Sudden emergence of a giant k-core in a random graph. J. Combin. Theory Ser. B 67 111–151.Google Scholar
[13]Pittel, B. and Wormald, N. (2003) Asymptotic enumeration of sparse graphs with a minimum degree constraint. J. Combin. Theory Ser. A 101 249–263.CrossRefGoogle Scholar
[14]Prałat, P., Verstraëte, J. and Wormald, N. (2011) On the threshold for k-regular subgraphs of random graphs. Combinatorica 31 565–581.Google Scholar
[15]Pretti, M. and Weigt, M. (2006) Sudden emergence of q-regular subgraphs in random graphs. Europhys. Lett. 75 8–14.Google Scholar