Article contents
Cycles in a Uniform Graph Process†
Published online by Cambridge University Press: 12 September 2008
Abstract
We study the asymptotic properties of a “uniform” random graph process 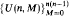 in which the minimum degree of U(n, M) grows at least as fast as ⌊M/n⌋. We show that if M — n → → ∞, almost surely U(n, M) consists of one giant component and some number of small unicyclic components. We go on to study the distribution of cycles in unicyclic components as they emerge at the beginning of the process and disappear when captured by the giant one.
in which the minimum degree of U(n, M) grows at least as fast as ⌊M/n⌋. We show that if M — n → → ∞, almost surely U(n, M) consists of one giant component and some number of small unicyclic components. We go on to study the distribution of cycles in unicyclic components as they emerge at the beginning of the process and disappear when captured by the giant one.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1992
References
- 6
- Cited by


