No CrossRef data available.
Article contents
Volume integral means over spherical shell
Published online by Cambridge University Press: 12 April 2021
Abstract
We investigate integral means over spherical shell of holomorphic functions in the unit ball
 $\mathbb {B}_n$
of
$\mathbb {B}_n$
of
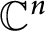 $\mathbb {C}^n$
with respect to the weighted volume measures and their relation with the weighted Hadamard product. The main result of this paper has many consequences which improve some well-known estimates related to the Hadamard product in Hardy spaces and weighted Bergman spaces.
$\mathbb {C}^n$
with respect to the weighted volume measures and their relation with the weighted Hadamard product. The main result of this paper has many consequences which improve some well-known estimates related to the Hadamard product in Hardy spaces and weighted Bergman spaces.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
Burbea, J. and Li, S. Y.,
Weighted Hadamard products of holomorphic functions in the ball
. Pac. J. Math. 168(1995), 235–270.CrossRefGoogle Scholar
Grauert, H. and Fritzsche, K.,
Several complex variables
. Springer, New York, 1976.CrossRefGoogle Scholar
Hadamard, J.,
Théorème sur les séries entières
. Acta Math. 22(1899), 55–63.10.1007/BF02417870CrossRefGoogle Scholar
Karapetrović, B. and Mashreghi, J.,
Hadamard convolution and area integral means in Bergman spaces
. Results Math. 75(2020), 1–11.CrossRefGoogle Scholar
Karapetrović, B. and Mashreghi, J.,
Hadamard products in weighted Bergman spaces
. J. Math. Anal. Appl. 494(2021), 1–17.CrossRefGoogle Scholar
Pavlović, M.,
An inequality for the integral means of a Hadamard product
. Proc. Amer. Math. Soc. 103(1988), 404–406.CrossRefGoogle Scholar
Range, R. M.,
Holomorphic functions and integral representations in several complex variables
. Springer, New York, 1986.CrossRefGoogle Scholar
Rudin, W., Function theory in the unit ball of
 ${\mathbb{C}}^n$
. Springer, New York, 1980.10.1007/978-3-540-68276-9CrossRefGoogle Scholar
${\mathbb{C}}^n$
. Springer, New York, 1980.10.1007/978-3-540-68276-9CrossRefGoogle Scholar
Tovstolis, A. V.,
Estimates for the Hadamard product on Hardy and Bergman spaces
. Analysis 34(2014), 243–256.CrossRefGoogle Scholar
Vukotić, D.,
A sharp estimate for
 ${A}_{\alpha}^p$
functions in
${A}_{\alpha}^p$
functions in
 ${\mathbb{C}}^n$
. Proc. Amer. Math. Soc. 117(1993), 753–756.Google Scholar
${\mathbb{C}}^n$
. Proc. Amer. Math. Soc. 117(1993), 753–756.Google Scholar
Xiao, J. and Zhu, K.,
Volume integral means of holomorphic functions
. Proc. Amer. Math. Soc. 139(2011), 1455–1465.CrossRefGoogle Scholar
Zhu, K.,
Translating inequalities between Hardy and Bergman spaces
. Amer. Math. Monthly 111(2004), no. 6, 520–525.CrossRefGoogle Scholar
Zhu, K.,
Spaces of Holomorphic Functions in the Unit Ball
. Graduate Texts in Mathematics, 226, Springer, New York, 2005.Google Scholar



