Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T17:20:38.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Variational principles for symplectic eigenvalues

Part of: Variational principles of physics General theory of linear operators Basic linear algebra

Published online by Cambridge University Press:  20 August 2020

Rajendra Bhatia  and
Tanvi Jain
Rajendra Bhatia
Affiliation:
Ashoka University, SonepatHaryana131029, India e-mail: [email protected]
Tanvi Jain*
Affiliation:
Indian Statistical Institute, New Delhi110016, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

If A is a real $2n \times 2n$ positive definite matrix, then there exists a symplectic matrix M such that 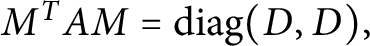$M^TAM=\text {diag}(D, D),$ where D is a positive diagonal matrix with diagonal entries $d_1(A)\leqslant \cdots \leqslant d_n(A).$ We prove a maxmin principle for 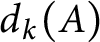$d_k(A)$ akin to the classical Courant–Fisher–Weyl principle for Hermitian eigenvalues and use it to derive an analogue of the Weyl inequality 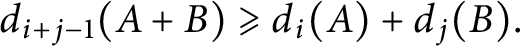$d_{i+j-1}(A+B)\geqslant d_i(A)+d_j(B).$

Keywords

Symplectic eigenvaluesmaxmin principleWeyl’s inequalities

MSC classification

Primary: 15A45: Miscellaneous inequalities involving matrices
Secondary: 47A75: Eigenvalue problems 49S05: Variational principles of physics (should also be assigned at least one other classification number in section 49)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 3 , September 2021 , pp. 553 - 559
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work of RB is supported by a Bhatnagar Fellowship of the CSIR. TJ acknowledges financial support from SERB MATRICS grant number MTR/2018/000554.

References

Dutta, Arvind, B., Mukunda, N., and Simon, R., The real symplectic groups in quantum mechanics and optics . Pramana 45(1995), 471–495.Google Scholar
Bhatia, R., Matrix analysis . Graduate Texts in Mathematics, 169, Springer-Verlag, New York, 1997. http://dx.doi.org/10.1007/978-1-4612-0653-8 CrossRefGoogle Scholar
Bhatia, R., Linear algebra to quantum cohomology: The story of Alfred Horn’s inequalities . Amer. Math. Monthly 108(2001), 289–318. http://dx.doi.org/10.2307/2695237 CrossRefGoogle Scholar
Bhatia, R., Some inequalities for eigenvalues and symplectic eigenvalues of positive definite matrices . Int. J. Math. 30(2019), 1950055. http://dx.doi.org/10.1142/s0129167x19500551 CrossRefGoogle Scholar
Bhatia, R. and Jain, T., On symplectic eigenvalues of positive definite matrices . J. Math. Phys. 56(2015), 112201. http://dx.doi.org/10.1063/1.493582 CrossRefGoogle Scholar
Bhatia, R. and Jain, T., A Schur-Horn theorem for symplectic eigenvalues . Linear Algebra Appl. 599(2020), 133–139. http://dx.doi.org/10.1016/j.laa.2020.04.005 CrossRefGoogle Scholar
de Gosson, M., Symplectic geometry and quantum mechanics . Operator Theory: Advances and Applications, 166, Advances in Partial Differential Equations (Basel), Birkhäuser, Verlag, Basel, 2006. http://dx.doi.org/10.1007/3-7643-7575-2 CrossRefGoogle Scholar
Hiroshima, T., Additivity and multiplicativity properties of some Gaussian channels for Gaussian inputs . Phys. Rev. A 73(2006), 012330.CrossRefGoogle Scholar
Hofer, H. and Zehnder, E., Symplectic invariants and Hamiltonian dynamics . Modern Birkhäuser Classics, Birkhäuser Verlag, Basel, 2011. http://dx.doi.org/10.1007/978-3-0348-0104-1 CrossRefGoogle Scholar
Eisert, J., Tyc, T., Rudolph, T., Sanders, B. C., Gaussian quantum marginal problem . Comm. Math. Phys. 280(2008), 263–280. http://dx.doi.org/10.1007/s00220-008-0442-4 CrossRefGoogle Scholar
Jain, T. and Mishra, H. K., Derivatives of symplectic eigenvalues and a Lidskii type theorem. Preprint, 2020. arXiv:2004.11024 CrossRefGoogle Scholar
Krbek, M., Tyc, T., and Vlach, J., Inequalities for quantum marginal problems with continuous variables . J. Math. Phys. 55(2014), 062201–7. http://dx.doi.org/10.1063/1.4880198 CrossRefGoogle Scholar