Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T07:28:48.207Z Has data issue: false hasContentIssue false
  • English
  • Français

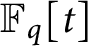Vanishing of multizeta values over $\mathbb {F}_q[t]$ at negative integers

Part of: Zeta and $L$-functions: analytic theory Algebraic number theory: global fields

Published online by Cambridge University Press:  18 January 2021

Shuhui Shi
Shuhui Shi*
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX77843, USA
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

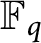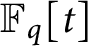Let $\mathbb {F}_q$ be the finite field of q elements. In this paper, we study the vanishing behavior of multizeta values over $\mathbb {F}_q[t]$ at negative integers. These values are analogs of the classical multizeta values. At negative integers, they are series of products of power sums 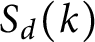$S_d(k)$ which are polynomials in t. By studying the t-valuation of 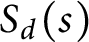$S_d(s)$ for 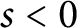$s < 0$ , we show that multizeta values at negative integers vanish only at trivial zeros. The proof is inspired by the idea of Sheats in the proof of a statement of “greedy element” by Carlitz.

Keywords

multizeta valuesvanishing at negative integerstrivial zeropower sumvaluation monotonicitymodest element

MSC classification

Primary: 11M32: Multiple Dirichlet series and zeta functions and multizeta values
Secondary: 11M38: Zeta and $L$-functions in characteristic $p$ 11R58: Arithmetic theory of algebraic function fields
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 1 , March 2022 , pp. 9 - 29
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2021

References

Böckle, G., The distribution of the zeros of the Goss zeta-function for $A={F}_2\left[x,y\right]/ \left({y}^2+y+{x}^3+x+1\right)$ . Math. Z. 275(2013), nos. 3–4, 835–861.10.1007/s00209-013-1162-9CrossRefGoogle Scholar
Broadhurst, D. J. and Kreimer, D., Association of multiple zeta values with positive knots via Feynman diagrams up to $9$ loops . Phys. Lett. B. 393(1997), nos. 3–4, 403–412.CrossRefGoogle Scholar
Burgos Gil, J. I. and Fresán, J., Multiple zeta values: from numbers to motives, to appear in Clay Mathematics Proceedings. http://javier.fresan.perso.math.cnrs.fr/mzv.pdf.Google Scholar
Carlitz, L., Finite sums and interpolation formulas over $GF\left[{p}^n,x\right]$ . Duke Math. J. 15(1948), 1001–1012.CrossRefGoogle Scholar
Chang, C.-Y., On characteristic p multizeta values, Algebraic number theory and related topics 2012 . RIMS Kôkyûroku Bessatsu, B51, Research Institute For Mathematical Sciences, Kyoto, 2014, pp. 177–202.Google Scholar
Deligne, P. and Goncharov, A. B., Groupes fondamentaux motiviques de Tate mixte . Ann. Sci. École Norm. Sup. 38(2005), no. 1, 1–56, Series 4.CrossRefGoogle Scholar
Diaz-Vargas, J., Riemann hypothesis for ${F}_p\left[T\right]$ . J. Number Theory 59(1996), no. 2, 313–318.CrossRefGoogle Scholar
Euler, L., Meditationes circa singulare serierum genus . Novi Comm. Acad. Sci. Petropol. 20(1775), 140–186, Reprinted in “Opera Omnia”, ser. 1, vol. 15, B. G. Teubner, Berlin, 1927, pp. 217–267.Google Scholar
Furusho, H., Komori, Y., Matsumoto, K., and Tsumura, H., Desingularization of complex multiple zeta-functions . Amer. J. Math. 139(2017), no. 1, 147–173.10.1353/ajm.2017.0002CrossRefGoogle Scholar
Goncharov, A. B., Multiple ζ-values, Galois groups, and geometry of modular varieties . In: European Congress of Mathematics, Vol. I (Barcelona, 2000), Progr. Math., 201, Birkhäuser, Basel, 2001, pp. 361–392.Google Scholar
Goncharov, A. B., Galois symmetries of fundamental groupoids and noncommutative geometry . Duke Math. J. 128(2005), no. 2, 209–284.CrossRefGoogle Scholar
Goss, D., $v$ -Adic zeta functions, $L$ -series and measures for function fields . Invent. Math. 55(1979), 107–119.10.1007/BF01390084CrossRefGoogle Scholar
Goss, D., Basic structures of function field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 35, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
Hoffman, M. E., Multiple harmonic series . Pacific J. Math. 152(1992), no. 2, 275–290.10.2140/pjm.1992.152.275CrossRefGoogle Scholar
Masri, R., Multiple zeta values over global function fields . In: Multiple Dirichlet series, automorphic forms, and analytic number theory, Proc. Sympos. Pure Math., 75, American Mathematical Society, Providence, RI, 2006, pp. 157–175.Google Scholar
Sheats, J. T., The Riemann hypothesis for the Goss zeta function for ${\textbf{F}}_q\left[T\right]$ . J. Number Theory 71(1998), no. 1, 121–157.10.1006/jnth.1998.2232CrossRefGoogle Scholar
Thakur, D. S., Function field arithmetic. World Scientific Publishing, River Edge, NJ, 2004.CrossRefGoogle Scholar
Thakur, D. S., Power sums with applications to multizeta and zeta zero distribution for ${F}_q\left[t\right]$ . Finite Fields Appl. 15(2009), no. 4, 534–552.10.1016/j.ffa.2009.04.002CrossRefGoogle Scholar
Thakur, D. S., Multizeta values for function fields: a survey . J. Théor. Nombres Bordeaux 29(2017), no. 3, 997–1023.CrossRefGoogle Scholar
Zagier, D., Values of zeta functions and their applications. In: First European Congress of Mathematics, Vol. II (Paris, 1992), Progr. Math., 120, Birkhäuser, Basel, 1994, pp. 497–512.Google Scholar