Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Levin, Eli
and
Lubinsky, Doron
2016.
Universality in measure in the bulk for varying weights.
Michigan Mathematical Journal,
Vol. 65,
Issue. 4,
Alpan, G.
2016.
Spacing properties of the zeros of orthogonal polynomials on Cantor sets via a sequence of polynomial mappings.
Acta Mathematica Hungarica,
Vol. 149,
Issue. 2,
p.
509.
Simanek, Brian
2017.
Two universality results for polynomial reproducing kernels.
Journal of Approximation Theory,
Vol. 216,
Issue. ,
p.
16.
Lubinsky, D. S.
2017.
Approximation Theory XV: San Antonio 2016.
Vol. 201,
Issue. ,
p.
219.
Levin, Eli
and
Lubinsky, Doron S.
2018.
Bounds and Asymptotics for Orthogonal Polynomials for Varying Weights.
p.
153.
Lubinsky, D.
2019.
Local asymptotics for orthonormal polynomials in the interior of the support via universality.
Proceedings of the American Mathematical Society,
Vol. 147,
Issue. 9,
p.
3877.
Lubinsky, Doron S.
2020.
Local asymptotics for orthonormal polynomials on the unit circle via universality.
Journal d'Analyse Mathématique,
Vol. 141,
Issue. 1,
p.
285.
Totik, V.
2020.
Oscillatory behavior of orthogonal polynomials.
Acta Mathematica Hungarica,
Vol. 160,
Issue. 2,
p.
453.
Levin, Eli
and
Lubinsky, Doron S.
2020.
Local limits for orthogonal polynomials for varying measures via universality.
Journal of Approximation Theory,
Vol. 254,
Issue. ,
p.
105394.
Bessonov, R.V.
2021.
Entropy function and orthogonal polynomials.
Journal of Approximation Theory,
Vol. 272,
Issue. ,
p.
105650.
Lubinsky, Doron Shaul
2022.
Нули, оценки и асимптотики для ортогональных полиномов на единичной окружности.
Математический сборник,
Vol. 213,
Issue. 11,
p.
31.
Świderski, Grzegorz
and
Van Assche, Walter
2022.
Christoffel functions for multiple orthogonal polynomials.
Journal of Approximation Theory,
Vol. 283,
Issue. ,
p.
105820.
Lubinsky, Doron Shaul
2022.
On zeros, bounds, and asymptotics for orthogonal polynomials on the unit circle.
Sbornik: Mathematics,
Vol. 213,
Issue. 11,
p.
1512.
Levin, Eli
and
Lubinsky, D.S.
2022.
Asymptotics for orthogonal polynomials and separation of their zeros.
Journal of Approximation Theory,
Vol. 281-282,
Issue. ,
p.
105804.
Levin, Eli
and
Lubinsky, D. S.
2023.
Exploring Mathematical Analysis, Approximation Theory, and Optimization.
Vol. 207,
Issue. ,
p.
177.
Bessonov, Roman
2024.
On Rate of Convergence for Universality Limits.
Integral Equations and Operator Theory,
Vol. 96,
Issue. 1,
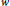 $w$
. With a new inequality for polynomials and with the use of fast decreasing polynomials, it is shown that an approach of D. S. Lubinsky is applicable. The proof works at all points that are Lebesgue-points for both the weight function
$w$
. With a new inequality for polynomials and with the use of fast decreasing polynomials, it is shown that an approach of D. S. Lubinsky is applicable. The proof works at all points that are Lebesgue-points for both the weight function
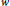 $w$
and
$w$
and
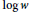 $\log \,w$
.
$\log \,w$
.

