No CrossRef data available.
Article contents
A Stochastic Ergodic Theorem for General Additive Processes
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this article, we obtain the stochastic ergodic theorem for general additive processes. That is, we prove that there exists 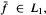 , such that
, such that 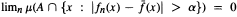 whenever α > 0 and A is a measurable set with μ(A) < ∞, where
whenever α > 0 and A is a measurable set with μ(A) < ∞, where 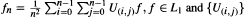 and {U(ij)}} an arbitrary (two dimensional) semigroup of L1 -contractions. This result generalizes the stochastic ergodic theorem (SET) of U. Krengel and the SET of M. A. Akcoglu and L. Sucheston.
and {U(ij)}} an arbitrary (two dimensional) semigroup of L1 -contractions. This result generalizes the stochastic ergodic theorem (SET) of U. Krengel and the SET of M. A. Akcoglu and L. Sucheston.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1989
References
1.
Akcoglu, M. A. and Sucheston, L., A stochastic ergodic theorem for superadditive processes, Erg. Th. & Dynam. System., 3, 335–344, (1983).Google Scholar
2.
Brunei, A., Théorème ergodique ponctuel pour un semi-groupe commutatif finiment engendré de contractions de L\, Ann. Inst. Henri Poincare, Sect. B, 9, 327–343, (1973).Google Scholar
3.
Chacon, R. V. and Krengel, U., Linear modulus of a linear operator, Proc. A.M.S., 15, 553–559, (1966).Google Scholar
5.
Krengel, U., On the global limit behaviour of Markov chains and of general non-singular Markov processes, Z. Wahr., 6, 302–316, (1966).Google Scholar


