Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-20T05:56:49.835Z Has data issue: false hasContentIssue false
  • English
  • Français

The Spectrum and Isometric Embeddings of Surfaces of Revolution

Published online by Cambridge University Press:  20 November 2018

Martin Engman
Martin Engman*
Affiliation:
Departamento de Ciencias y Tecnología, Universidad Metropolitana, San Juan, Puerto Rico 00928 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A sharp upper bound on the first 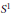${{S}^{1}}$ invariant eigenvalue of the Laplacian for 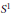${{S}^{1}}$ invariant metrics on 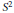${{S}^{2}}$ is used to find obstructions to the existence of 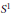${{S}^{1}}$ equivariant isometric embeddings of such metrics in (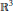${{\mathbb{R}}^{3}}$, can). As a corollary we prove: If the first four distinct eigenvalues have even multiplicities then the metric cannot be equivariantly, isometrically embedded in (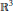${{\mathbb{R}}^{3}}$, can). This leads to generalizations of some classical results in the theory of surfaces.

Keywords

58J5058J5353C2035P15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 2 , 01 June 2006 , pp. 226 - 236
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Abreu, M. and Freitas, P., On the invariant spectrum of S 1 -invariant metrics on S 2 . Proc. London Math. Soc. 84(2002), 213–230.Google Scholar
[2] Alexandrov, A., Vnutrennyaya Geometriya Vypuklyh PoverhnosteĬ. OGIZ Moscow, 1948.Google Scholar
[3] Besse, A., Manifolds All of Whose Geodesics are Closed. Ergebnisse der Mathematik und ihrer Grenzgebiete 93, Springer-Verlag, Berlin, 1978.Google Scholar
[4] Chen, B.-Y., A report on submanifolds of finite type. Soochow J. Math. 22(1996), no. 2, 117–337.Google Scholar
[5] Engman, M., New spectral characterization theorems for S 2 . Pacific J. Math. 154(1992), no. 2, 215–229.Google Scholar
[6] Engman, M., Trace formulae for S 1 invariant Green's operators on S 1 . Manuscripta Math. 93(1997), no. 3, 357–368.Google Scholar
[7] Engman, M., Sharp bounds for eigenvalues and multiplicities on surfaces of revolution. Pacific J. Math. 186(1998), no. 1, 29–37.Google Scholar
[8] Engman, M., A note on isometric embeddings of surfaces of revolution. Amer.Math. Monthly 111(2004), no. 3, 251–255.Google Scholar
[9] Greene, R., Metrics and isometric embeddings of the 2-sphere. J. Differential Geometry 5(1971), 353–356.Google Scholar
[10] Guan, P. and Li, Y. Y., The Weyl problem with nonnegative Gauss curvature. J. Differential Geometry 39(1994), 331–342.Google Scholar
[11] Heinz, E., On Weyl's embedding problem. J. Math. Mech. 11(1962), 421–454.Google Scholar
[12] Hersch, M. J., Quatre propriétés isopérimétriques de membranes sphériques homogènes. C. R. Acad. Sci. Paris Sér. A-B 270(1970), A1645–A1648.Google Scholar
[13] Hong, J. and Zuily, C., Isometric embedding of the 2-sphere with non negative curvature in ℝ3 . Math. Z. 219(1995), no. 3, 323–334.Google Scholar
[14] Hwang, A. D., A Symplectic Look at Surfaces of Revolution. Enseign. Math. (2) 49(2003), no. 1-2, 157–172.Google Scholar
[15] Hwang, A. and Singer, M., A momentum construction for circle-invariant Kähler metrics. Trans. Amer.Math. Soc. 354(2002), 2285–2325.Google Scholar
[16] Kobayashi, S., Transformation Groups in Differential Geometry. Reprint of the 1972 edition. Classics in Mathematics. Springer-Verlag, Heidelberg, 1995.Google Scholar
[17] Lewy, H., A priori limitations for solutions of Monge–Ampère equations. Trans. Amer. Math. Soc. (3) 37(1935), no. 3, 417–434.Google Scholar
[18] Li, P. and Yau, S. T., A new conformal invariant and its applications to theWillmore Conjecture and the first eigenvalue of compact surfaces. Invent. Math. 69(1982), no. 2, 269–291.Google Scholar
[19] Nirenberg, L., The Weyl and Minkowski problems in differential geometry in the large. Comm. Pure Appl. Math 6(1953), 337–394.Google Scholar
[20] Pogorelov, A. V., Deformation of convex surfaces. Gosudarstv. Izdat. Tehn.-Teor. Lit., Moscow, 1951.Google Scholar
[21] Pogorelov, A. V., Extrinsic geometry of convex surfaces. Translations of Mathematical Monographs 35, American Mathematical Society, Providence, RI, 1973.Google Scholar
[22] Weyl, H., Über die Bestimmung einer geschlossen konvexen Fläche durch ihr Linienelement. Vierteljahrschrift Naturforsch. Gesell, Zürich, 61(1916), 40–72.Google Scholar
[23] Yau, S. T., Survey on partial differential equations in differential geometry. In: Seminar on Differential Geometry, Ann. of Math. Stud. 102, Princeton University Press, Princeton, NJ, 1982, pp. 3–71..Google Scholar