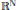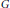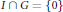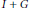Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wnuk, Witold
2015.
A note on the sum of closed ideals and Riesz subspaces.
Positivity,
Vol. 19,
Issue. 1,
p.
137.
Oikhberg, Timur
2016.
A note on latticeability and algebrability.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 1,
p.
523.