Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2025-01-01T05:21:30.430Z Has data issue: false hasContentIssue false
  • English
  • Français

A Singular Integral on L2(Rn)

Published online by Cambridge University Press:  20 November 2018

Dashan Fan
Dashan Fan*
Affiliation:
Department of Mathematical Sciences, University of Wisconsin-Milwaukee Milwaukee, Wisconsin 53201 U.S.A. e-mail:, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a convolution singular integral operator 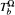associated to a kernel K(x) = b(x)Ω(x)|x|-n, and prove that if b ∊ L∞(ℝn) is a radial function and Ω ∊ H(Σn-1) with mean zero condition (1), then 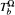is a bounded linear operator in the space L2(ℝn).

Keywords

42B99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 2 , 01 June 1994 , pp. 197 - 201
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Calderon, A. P. and Zygmund, A., On the existence of certain singular integrals, Acta. Math. 88(1952), 85–139.Google Scholar
2. Calderon, A. P. and Zygmund, A., On singular integrals, Amer. J. Math. 18(1956), 289–309.Google Scholar
3. Chen, K., On a singular integral, Studia Math. LXXXV(1987), 61–72.Google Scholar
4. Coifman, R. and Weiss, G., Extension of Hardy spaces and their use in analysis, Bull. Amer. Math. Soc. 83(1977), 569–645.Google Scholar
5. Colzani, L., Hardy spaces on Sphere, thesis, Ph. D., Washington University, St. Louis, 1982.Google Scholar
6. Fefferman, R., A note on singular integrals, Proc. Amer. Math. Soc. 74(1979), 266–270.Google Scholar
7. Lu, S., Taibleson, M. and Weiss, G., Space Generated by Blocks, Beijing Normal University Mathematics Series, Beijian Normal University Press, 1989.Google Scholar
8. Torchinsky, A., Real-variable Methods in Harmonic Analysis, Academic Press, 1986.Google Scholar