No CrossRef data available.
Article contents
A Short Note on the Higher Level Version of the Krull–Baer Theorem
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Klep and Velušček generalized the Krull–Baer theorem for higher level preorderings to the non-commutative setting. A 
$n$-real valuation 
$v$ on a skew field 
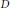$D$ induces a group homomorphism 
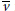$\overline{v}$. A section of 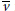$\overline{v}$ is a crucial ingredient of the construction of a complete preordering on the base field 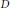$D$ such that its projection on the residue skew field 
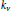${{k}_{v}}$ equals the given level 1 ordering on 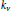${{k}_{v}}$. In the article we give a proof of the existence of the section of 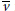$\overline{v}$, which was left as an open problem by Klep and Velušček, and thus complete the generalization of the Krull–Baer theorem for preorderings.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
[1] Becker, E., Summen n-ter Potenzen in Körpern. J. Reine Angew. Math.
307/308(1979), 8–30.Google Scholar
[2] Klep, I., Velušček, D., n-real valuations and the higher level version of the Krull–Baer theorem. J. Algebra
279(2004), no. 1, 345–361. doi:10.1016/j.jalgebra.2004.05.012Google Scholar
[3] Fuchs, L., Infinite abelian groups. Vol. I. Pure and Applied Mathematics, 36, Academic Press, New York-London, 1970.Google Scholar
[4] Schilling, O. F. G., The theory of valuations, Mathematical Surveys, 4, American Mathematical Society, New York, 1950.Google Scholar
[5] Powers, V., Holomorphy rings and higher level orders on skew fields. J. Algebra
136(1991), no. 1, 51–59. doi:10.1016/0021-8693(91)90063-EGoogle Scholar
You have
Access