No CrossRef data available.
Article contents
The shape of cyclic number fields
Published online by Cambridge University Press: 06 September 2022
Abstract
Let
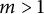 $m>1$
and
$m>1$
and
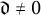 $\mathfrak {d} \neq 0$
be integers such that
$\mathfrak {d} \neq 0$
be integers such that
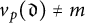 $v_{p}(\mathfrak {d}) \neq m$
for any prime p. We construct a matrix
$v_{p}(\mathfrak {d}) \neq m$
for any prime p. We construct a matrix
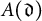 $A(\mathfrak {d})$
of size
$A(\mathfrak {d})$
of size
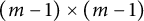 $(m-1) \times (m-1)$
depending on only of
$(m-1) \times (m-1)$
depending on only of
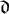 $\mathfrak {d}$
with the following property: For any tame
$\mathfrak {d}$
with the following property: For any tame
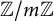 $ \mathbb {Z}/m \mathbb {Z}$
-number field K of discriminant
$ \mathbb {Z}/m \mathbb {Z}$
-number field K of discriminant
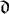 $\mathfrak {d}$
, the matrix
$\mathfrak {d}$
, the matrix
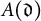 $A(\mathfrak {d})$
represents the Gram matrix of the integral trace-zero form of K. In particular, we have that the integral trace-zero form of tame cyclic number fields is determined by the degree and discriminant of the field. Furthermore, if in addition to the above hypotheses, we consider real number fields, then the shape is also determined by the degree and the discriminant.
$A(\mathfrak {d})$
represents the Gram matrix of the integral trace-zero form of K. In particular, we have that the integral trace-zero form of tame cyclic number fields is determined by the degree and discriminant of the field. Furthermore, if in addition to the above hypotheses, we consider real number fields, then the shape is also determined by the degree and the discriminant.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society



