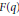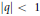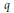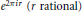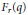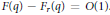Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Srivastava, Bhaskar
and
Costin, Rodica
2009.
A Mock Theta Function of Second Order.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2009,
Issue. 1,
Bringmann, Kathrin
Hikami, Kazuhiro
and
Lovejoy, Jeremy
2011.
On the modularity of the unified WRT invariants of certain Seifert manifolds.
Advances in Applied Mathematics,
Vol. 46,
Issue. 1-4,
p.
86.
ALFES, CLAUDIA
BRINGMANN, KATHRIN
and
LOVEJOY, JEREMY
2011.
Automorphic properties of generating functions for generalized odd rank moments and odd Durfee symbols.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 151,
Issue. 3,
p.
385.
Gordon, Basil
and
McIntosh, Richard J.
2012.
Partitions, q-Series, and Modular Forms.
Vol. 23,
Issue. ,
p.
95.
CHAN, SONG HENG
and
MAO, RENRONG
2012.
TWO CONGRUENCES FOR APPELL–LERCH SUMS.
International Journal of Number Theory,
Vol. 08,
Issue. 01,
p.
111.
Andrews, George E.
2013.
Concave and convex compositions.
The Ramanujan Journal,
Vol. 31,
Issue. 1-2,
p.
67.
Lovejoy, Jeremy
and
Osburn, Robert
2013.
The Bailey chain and mock theta functions.
Advances in Mathematics,
Vol. 238,
Issue. ,
p.
442.
Hickerson, Dean R.
and
Mortenson, Eric T.
2014.
Hecke-type double sums, Appell-Lerch sums, and mock theta functions, I.
Proceedings of the London Mathematical Society,
Vol. 109,
Issue. 2,
p.
382.
Rhoades, Robert C.
2014.
Asymptotics for the Number of Strongly Unimodal Sequences.
International Mathematics Research Notices,
Vol. 2014,
Issue. 3,
p.
700.
Chen, Bin
and
Zhou, Haigang
2014.
Note on the problem of Ramanujan’s radial limits.
Advances in Difference Equations,
Vol. 2014,
Issue. 1,
Somashekara, D.D.
and
Narasimha Murthy, K.
2014.
Applications of an identity of Andrews.
Arab Journal of Mathematical Sciences,
Vol. 20,
Issue. 2,
p.
205.
Mao, Renrong
2015.
The $$M_{2}$$ M 2 -rank of partitions without repeated odd parts modulo $$6$$ 6 and $$10$$ 10.
The Ramanujan Journal,
Vol. 37,
Issue. 2,
p.
391.
Chern, Bobbie
and
Rhoades, Robert C
2015.
The Mordell integral, quantum modular forms, and mock Jacobi forms.
Research in Number Theory,
Vol. 1,
Issue. 1,
Chen, Bin
and
Zhou, Haigang
2016.
Bilateral series in terms of mixed mock modular forms.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
Bayad, A.
Somashekara, D. D.
and
Narasimha Murthy, K.
2016.
On finite forms of Bailey's 2ψ2 transformation formulae and their applications.
International Journal of Number Theory,
Vol. 12,
Issue. 08,
p.
2189.
Gu, Nancy S.S.
and
Liu, Jing
2016.
Families of multisums as mock theta functions.
Advances in Applied Mathematics,
Vol. 79,
Issue. ,
p.
98.
Kim, Byungchan
Lim, Subong
and
Lovejoy, Jeremy
2016.
Odd-balanced unimodal sequences and related functions: parity, mock modularity and quantum modularity.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 9,
p.
3687.
McIntosh, Richard J.
2018.
Some identities for Appell–Lerch sums and a universal mock theta function.
The Ramanujan Journal,
Vol. 45,
Issue. 3,
p.
767.
McIntosh, Richard J.
2018.
New mock theta conjectures Part I.
The Ramanujan Journal,
Vol. 46,
Issue. 2,
p.
593.
Andrews, George E.
and
Berndt, Bruce C.
2018.
Ramanujan's Lost Notebook.
p.
249.