Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T19:01:20.003Z Has data issue: false hasContentIssue false
  • English
  • Français

The Saddle-Point Method and the Li Coefficients

Published online by Cambridge University Press:  20 November 2018

Kamel Mazhouda
Kamel Mazhouda*
Affiliation:
Faculté des sciences de Monastir, Département de mathématiques, 5000 Monastir, Tunisiae-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we apply the saddle-point method in conjunction with the theory of the Nörlund–Rice integrals to derive precise asymptotic formula for the generalized Li coefficients established by Omar and Mazhouda. Actually, for any function $F$ in the Selberg class 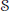$\mathcal{S}$ and under the Generalized Riemann Hypothesis, we have

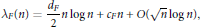$${{\lambda }_{F}}(n)\,=\,\frac{{{d}_{F}}}{2}n\,\log \,n\,+\,{{c}_{F}}n\,+\,O(\sqrt{n}\,\log \,n),$$

with

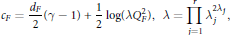$${{c}_{F}}\,=\,\frac{{{d}_{F}}}{2}(\gamma \,-\,1)\,+\,\frac{1}{2}\log (\lambda \text{Q}_{F}^{2}),\,\,\lambda \,=\,\prod\limits_{j=1}^{r}{\lambda _{j}^{2{{\lambda }_{j}}}},$$

where $\gamma $ is the Euler's constant and the notation is as below.

Keywords

11M4111M06Selberg classSaddle-point methodRiemann HypothesisLi's criterion
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 2 , 01 June 2011 , pp. 316 - 329
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Bombieri, E. and Hejhal, D. A., On the distribution of zeros of linear combinations of Euler products. Duke. Math. J. 80(1995), no. 3, 821–862. doi:10.1215/S0012-7094-95-08028-4Google Scholar
[2] Bombieri, E. and Lagarias, J. C., Complements to Li's criterion for the Riemann hypothesis. J. Number Theory 77(1999), no. 2, 274–287. doi:10.1006/jnth.1999.2392Google Scholar
[3] Coffey, M. W., Relations and positivity results for the derivatives of the Riemann ξ function. J. Comput. Appl. Math. 166(2004), no. 2, 525–534. doi:10.1016/j.cam.2003.09.003Google Scholar
[4] Coffey, M. W., Toward verification of the Riemann hypothesis. Math. Phys. Anal. Geom. 8(2005), no. 3, 211–255. doi:10.1007/s11040-005-7584-9Google Scholar
[5] Flajolet, P. and Vepstas, L., On differences of zeta values. J. Comput. Appl. Math. 220(2008), no. 1–2, 58–73. doi:10.1016/j.cam.2007.07.040Google Scholar
[6] Kaczorowski, J. and Perelli, A., The Selberg class: a survey. In: Number theory in progress, 2, de Gruyter, Berlin, 1999, pp. 953–992.Google Scholar
[7] Lagarias, J. C., Li coefficients for automorphic L-functions. Ann. Inst. Fourier 57(2007), no. 5, 1689–1740.Google Scholar
[8] Li, X.-J., The positivity of a sequence of number and the Riemann hypothesis. J. Number Theory 65(1997), no. 2, 325–333. doi:10.1006/jnth.1997.2137Google Scholar
[9] Li, X.-J., Explicit formulas for Dirichlet and Hecke L-functions. Illinois J. Math. 48(2004), no. 2, 491–503.Google Scholar
[10] Maslanka, K., Effective method of computing Li's coefficients and their properties. Experimental Math., to appear.Google Scholar
[11] Omar, S. and Mazhouda, K., Le critère de Li et l’hypothèse de Riemann pour la classe de Selberg. J. Number Theory 125(2007), no. 1, 50–58. doi:10.1016/j.jnt.2006.09.013Google Scholar
[12] Omar, S. and Mazhouda, K., Le critère de positivité de Li pour la classe de Selberg. C. R. Acad. Sci. Paris 345(2007), no. 5, 245–248.Google Scholar
[13] Omar, S. and Mazhouda, K., Corrigendum et addendum à Le critère de Li et l’hypothèse de Riemann pour la classe de Selberg [J. Number Theory 125(2007), no. 1, 50–58]. J. Number Theory 130(2010), no. 4, 1109–1114. doi:10.1016/j.jnt.2009.10.010Google Scholar
[14] Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and radom matrix theory. Duke. Math. J. 81(1996), no. 2, 269–322. doi:10.1215/S0012-7094-96-08115-6Google Scholar
[15] Selberg, A., Old and new conjectures and results about a class of Dirichlet series. In: Proceedings of the Amalfi conference on analytic number theory (Maiori, 1989), Univ. Salermo, 1992, pp. 367–385.Google Scholar
[16] Srinivas, K., Distinct zeros of functions in the Selberg class. Acta. Arith. 103(2002), no. 3, 201–207. doi:10.4064/aa103-3-1Google Scholar
[17] Voros, A., A sharpening of Li's criterion for the Riemann hypothesis. Math. Phys. Anal. Geom. 9(2006), no. 1, 53–63. doi:10.1007/s11040-005-9002-8Google Scholar