Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T23:53:13.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramification des séries formelles

Published online by Cambridge University Press:  20 November 2018

François Laubie
François Laubie*
Affiliation:
UMR6090 CNRS Université de Limoges Département de Mathématiques 123 Av. Albert Thomas 87060 Limoges Cedex France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 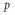$p$ be a prime number. Let 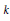$k$ be a finite field of characteristic 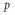$p$. The subset 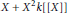$X\,+\,{{X}^{2}}k[[X]]$ of the ring 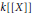$k\left[\!\left[ X \right]\!\right]$ is a group under the substitution law $\circ $ sometimes called the Nottingham group of 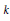$k$, it is denoted by 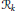${{\mathcal{R}}_{k}}$. The ramification of one series 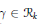$\gamma \,\in \,{{\mathcal{R}}_{k}}$ is caracterized by its lower ramification numbers: 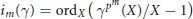${{i}_{m}}(\gamma )\,=\,\text{or}{{\text{d}}_{X}}({{\gamma }^{{{p}^{m}}}}\,(X)/X-1)\,$, as well as its upper ramification numbers:

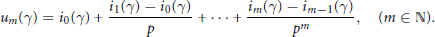$${{u}_{m}}(\gamma )\ =\ {{i}_{0}}(\gamma )+\frac{{{i}_{1}}(\gamma )-{{i}_{0}}(\gamma )}{p}\,+\,.\,.\,.\,+\,\frac{{{i}_{m}}(\gamma )-{{i}_{m-1}}(\gamma )}{{{p}^{m}}},\,\,\,\,\,\,(m\,\in \,\mathbb{N}).$$

By Sen's theorem, the 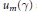${{u}_{m}}(\gamma )$ are integers. In this paper, we determine the sequences of integers (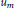${{u}_{m}}$) for which there exists 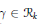$\gamma \,\in \,{{\mathcal{R}}_{k}}$ such that 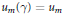${{u}_{m}}(\gamma )\,=\,{{u}_{m}}$ for all integer 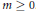$m\,\ge \,0$.

Keywords

11S1520E18ramificationNottingham group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 2 , 01 June 2004 , pp. 237 - 245
Copyright
Copyright © Canadian Mathematical Society 2004

References

Réféences

[1] Camina, R. D., Subgroups of the Nottingham group. J. Algebra 196 (1997), 101–113.Google Scholar
[2] Fontaine, J.-M., Groupes de ramification et représentation d'Artin. Ann. Sci. École Norm. Sup 4 (1971), 337–392.Google Scholar
[3] Laubie, F. and Saine, M., Ramification of some automorphisms of local fields. J. Number Theory 72 (1998), 174–182.Google Scholar
[4] Marshall, M. A., Ramification groups of Abelian local field extensions. Canad. J. Math. 23 (1971), 271–281.Google Scholar
[5] Maus, E., Existenz p-adischer Zahlkörper zu Vorgegebenem Verzweigungsverhalten. Dissertation, Hamburg, 1965.Google Scholar
[6] Miki, H., On the ramification numbers of cyclic p-extensions over local fields. J. Reine Angew.Math. 328 (1981), 99–115.Google Scholar
[7] Sen, S., On automorphisms of local fields. Ann. of Math 90 (1969), 33–46.Google Scholar
[8] Serre, J.-P., Corps locaux. 2-ème ed., Hermann, Paris, 1968.Google Scholar
[9] Tate, J., p-divisible groups. Proc. of a conference on local fields, Driebergen, 1966.Google Scholar
[10] Wintenberger, J.-P., Extensions de Lie et groupes d'automorphismes des corps locaux de caractéristique p. C. R. Acad. Sci. Sér. A 288(1979) 477–479.Google Scholar
[11] Wintenberger, J.-P., Extensions abéliennes et groupes d'automorphismes de corps locaux. C. R. Acad. Sci. Paris Sér. A.B 290 (1980), 201–203.Google Scholar
[12] Wintenberger, J.-P., Le corps des normes de certaines extensions infinies de corps locaux ; applications. Ann. Sci. École Norm. Sup. 16 (1983), 59–89.Google Scholar
[13] Wintenberger, J.-P., Automorphismes de corps locaux de caractéristique p. (2002), preprint.Google Scholar
[14] Wyman, B. F., Wildly ramified gamma extensions. Amer. J. Math. 91 (1969), 135–152.Google Scholar