Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T05:26:12.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramification des groupes abéliens d’automorphismes des corps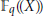

Published online by Cambridge University Press:  20 November 2018

François Laubie
François Laubie*
Affiliation:
Xlim UMR 6172 CNRS-Université de Limoges, Faculté des Sciences et techniques, 123, Avenue Albert Thomas, 87060 Limoges, Francee-mail’:[email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit $q$ une puissance d’un nombre premier 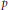$p$. Dans cette note on établit la généralisation suivante d’un théorème de Wintenberger : tout sous-groupe abélien fermé du groupe des 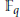${{\mathbb{F}}_{q}}$-automorphismes continus du corps des séries formelles 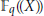${{\mathbb{F}}_{q}}((X\text{))}$ muni de sa filtration de ramification est un groupe filtré isomorphe au groupe de Galois d’une extension abélienne d’un corps local à corps résiduel 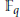${{\mathbb{F}}_{q}}$, filtré par les groupes de ramification de l’extension en numérotation inférieure.

Keywords

11S15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 594 - 597
Copyright
Copyright © Canadian Mathematical Society 2007

References

Références

[1] Marshall, M. A., Ramification groups of Abelian local field extensions. Canad. J. Math. 23(1971), no. 2, 278–281.Google Scholar
[2] Wintenberger, J.-P., Le corps des normes de certaines extensions infinies de corps locaux: applications. Ann. Sci. École Norm. Sup. 16(1983), no. 1, 59–89.Google Scholar
[3] Wintenberger, J.-P., Extensions abéliennes et groupes d’automorphismes des corps locaux. C. R. Acad. Sci. Paris Sér. A-B 290(1980), no. 5, A201–A203.Google Scholar
[4] Wintenberger, J.-P., Automorphismes et extensions galoisiennes de corps locaux. Thèse du troisième cycle, Institut Fourier, Université Scientifique et Médicale de Grenoble, 1978.Google Scholar