Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-12T19:47:11.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasisymmetrically Minimal Moran Sets

Published online by Cambridge University Press:  20 November 2018

Mei-Feng Dai
Mei-Feng Dai*
Affiliation:
Nonlinear Scientific Research Center, Faculty of Science, Jiangsu University, Zhenjiang, 212013, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

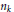M. Hu and S. Wen considered quasisymmetrically minimal uniform Cantor sets of Hausdorff dimension 1, where at the $K$-th set one removes from each interval $I$ a certain number ${{n}_{k}}$ of open subintervals of length 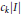${{c}_{k}}\left| I \right|$, leaving 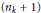$\left( {{n}_{k}}\,+\,1 \right)$ closed subintervals of equal length. Quasisymmetrically Moran sets of Hausdorff dimension 1 considered in the paper are more general than uniform Cantor sets in that neither the open subintervals nor the closed subintervals are required to be of equal length.

Keywords

28A8054C30quasisymmetricMoran setHausdorff dimension
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 292 - 305
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bishop, C. J., Quasiconformal mappings which increase dimension. Ann. Acad. Sci. Fenn. Math. 24(1999), no. 2, 397–407. Google Scholar
[2] Falconer, K., Fractal Geometry: Mathematical Foundation and Applications. JohnWiley & Sons, Chichester, 1990.Google Scholar
[3] Gehring, F.W. and Väisälä, J., Hausdorff dimension and quasiconformal mappings. Math. J. London Math. Soc. 6(1973), 504-512. http://dx.doi.org/10.1112/jlms/s2-6.3.504 Google Scholar
[4] Hakobyan, H. A., Cantor sets minimal for quasi-symmetric maps. J. Contemp. Math. Anal. 41(2006), no. 2, 5-13. Translated from the Russian.Google Scholar
[5] Hu, M. and Wen, S., Quasisymmetrically minimal uniform Cantor sets. Topology Appl. 155(2008), no. 6, 515–521. http://dx.doi.org/10.1016/j.topol.2007.10.006 Google Scholar
[6] Hua, S., The dimensions of generalized self-similar sets. (Chinese) Acta. Math. Appl. Sinica 17(1994), no. 4, 551–558. Google Scholar
[7] Kovalev, L. V., Conformal dimension does not assume values between 0 and 1. Duke Math. J. 134(2006), no. 1, 1–13. http://dx.doi.org/10.1215/S0012-7094-06-13411-7 Google Scholar
[8] Tukia, P., Hausdorff dimension and quasisymmetric mappings. Math. Scand. 65(1989), no. 1, 152–160. Google Scholar
[9] Tyson, J. T., Sets of minimal Hausdorff dimension for quasisiconformal maps. Proc. Amer. Math. Soc. 128(2000), no. 11, 3361–3367. http://dx.doi.org/10.1090/S0002-9939-00-05433-2 Google Scholar
[10] Wu, J. M., Null sets for doubling and dyadic doubling measures. Ann. Acad. Sci. Fenn. Ser. A I Math. 18(1993), no. 1, 77–91. Google Scholar