Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-10T23:47:35.147Z Has data issue: false hasContentIssue false
  • English
  • Français

Orbits and Stabilizers for Solvable Linear Groups

Published online by Cambridge University Press:  20 November 2018

Jeffrey M. Riedl
Jeffrey M. Riedl *
Affiliation:
Department of Mathematics, University of Akron, Akron, OH 44325-4002, U.S.A. e-mail: riedl@uakron.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend a result of Noritzsch, which describes the orbit sizes in the action of a Frobenius group $G$ on a finite vector space 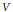$V$ under certain conditions, to a more general class of finite solvable groups $G$. This result has applications in computing irreducible character degrees of finite groups. Another application, proved here, is a result concerning the structure of certain groups with few complex irreducible character degrees.

Keywords

20B9920C1520C20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 2 , 01 June 2006 , pp. 285 - 295
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Huppert, B. and Manz, O., Degree problems I. Squarefree character degrees. Arch. Math. Basel 45(1985), no. 2, 125–132.Google Scholar
[2] Isaacs, I. M., Character Theory of Finite Groups. Dover, New York, 1994.Google Scholar
[3] Lewis, M. L. and Riedl, J. M., Affine semi-linear groups with three irreducible character degrees. J. Algebra 246(2001), no. 2, 708–720.Google Scholar
[4] Noritzsch, T., Groups having three complex irreducible character degrees. J. Algebra 175(1995), no. 3, 767–798.Google Scholar
[5] Riedl, J. M., Fitting heights of solvable groups with few character degrees. J. Algebra 233(2000), no. 1, 287–308.Google Scholar
[6] Riedl, J. M., Fitting heights of odd-order groups with few character degrees. J. Algebra 267(2003), no. 2, 421–442.Google Scholar