Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T18:52:12.769Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Modulii of Analytic Functions

Published online by Cambridge University Press:  20 November 2018

Malcolm J. Sherman
Malcolm J. Sherman*
Affiliation:
State University of New York, Albany, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem to be considered in this note, in its most concrete form, is the determination of all quartets f1, f2, g1, g2 of functions analytic on some domain and satisfying

*

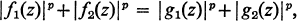
where p > 0. When p = 2 the question can be reformulated in terms of finding a necessary and sufficient condition for (two-dimensional) Hilbert space valued analytic functions to have equal pointwise norms, and the answer (Theorem 1) justifies this point of view. If p ≠ 2, the problem is solved by reducing to the case p = 2, and the reformulation in terms of the norm equality of lp valued analytic functions gives no clue to the answer.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 3 , September 1970 , pp. 325 - 327
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Day, M., Normed linear spaces, Academic Press, New York, 1962.Google Scholar
2. Nevanlinna, R. and Polya, G., Jahresbericht Deutsche Mathematikes Vereinigung 43 (1934), 6-7.Google Scholar