Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T04:20:51.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Moduli Space of a Spherical Polygonal Linkage

Published online by Cambridge University Press:  20 November 2018

Michael Kapovich  and
John J. Millson
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

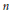We give a “wall-crossing” formula for computing the topology of the moduli space of a closed $n$-gon linkage on 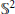${{\mathbb{S}}^{2}}$. We do this by determining the Morse theory of the function 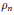${{\rho }_{n}}$ on the moduli space of 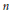$n$-gon linkages which is given by the length of the last side—the length of the last side is allowed to vary, the first 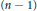$\left( n\,-\,1 \right)$ side-lengths are fixed. We obtain a Morse function on the 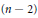$\left( n\,-\,2 \right)$-torus with level sets moduli spaces of 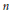$n$-gon linkages. The critical points of 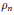${{\rho }_{n}}$ are the linkages which are contained in a great circle. We give a formula for the signature of the Hessian of 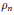${{\rho }_{n}}$ at such a linkage in terms of the number of back-tracks and the winding number. We use our formula to determine the moduli spaces of all regular pentagonal spherical linkages.

Keywords

14D2014P05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 3 , 01 September 1999 , pp. 307 - 320
Copyright
Copyright © Canadian Mathematical Society 1999

References

[A] Adler, V., Recuttings of polygons. Functional Anal. Appl. 27 (1993), 141–143.Google Scholar
[B] Berger, M., Geometry II. Universitext. Springer, New York, 1980.Google Scholar
[F] Foth, P., Deformations of representations of fundamental groups of open Kähler manifolds. Preprint, September, 1997.Google Scholar
[Ga] Gaffney, M., A special Stokes theorem for complete Riemannian manifolds. Ann. of Math. 60 (1954), 140–145.Google Scholar
[G] Galitzer, A., The moduli space of polygon linkages in the 2-sphere. Ph.D. thesis, University of Maryland, 1997.Google Scholar
[KK] Kirk, P. and Klassen, E., Representation spaces of Seifert fibered homology spheres. Topology 30 (1991), 77–95.Google Scholar
[KM1] Kapovich, M. and Millson, J. J., On the moduli space of polygons in the Euclidean plane. J. Differential Geom. 42 (1995), 133–164.Google Scholar
[KM2] Kapovich, M. and Millson, J. J., Hodge theory and the art of paper folding. Publ. Res. Inst.Math. Sci. 33(1997) 1–33.Google Scholar
[KM3] Kapovich, M. and Millson, J. J., The relative deformation theory of representations and flat connections and deformations of linkages in constant curvature spaces. Compositio Math. 103 (1996), 287–317.Google Scholar
[S] Sargent, M., Diffeomorphism equivalence of configuration spaces of polygons in constant curvature spaces. Ph.D. thesis, University of Maryland, 1995.Google Scholar