Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T10:39:21.885Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Membership in Bergman Spaces of the Derivative of a Blaschke Product With Zeros in a Stolz Domain

Published online by Cambridge University Press:  20 November 2018

Daniel Girela  and
José Ángel Peláez
Daniel Girela
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071 Málaga, Spain e-mail: [email protected] e-mail: [email protected]
José Ángel Peláez
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071 Málaga, Spain e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that the derivative of a Blaschke product whose zero sequence lies in a Stolz angle belongs to all the Bergman spaces 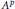${{A}^{P}}$ with 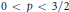$0<p<3/2$. The question of whether this result is best possible remained open. In this paper, for a large class of Blaschke products 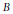$B$ with zeros in a Stolz angle, we obtain a number of conditions which are equivalent to the membership of 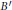${B}'$ in the space 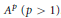${{A}^{p}}\left( p>1 \right)$. As a consequence, we prove that there exists a Blaschke product 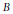$B$ with zeros on a radius such that 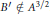${B}'\,\notin \,{{A}^{3/2}}$.

Keywords

30D5030D5532A36Blaschke productsHardy spacesBergman spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 3 , 01 September 2006 , pp. 381 - 388
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Ahern, P., The mean modulus and the derivative of an inner function. Indiana Univ. Math. J. 28(1979), no. 2, 311–347.Google Scholar
[2] Ahern, P. and Clark, D., On inner functions with Hp derivative. Michigan Math. J. 21(1974), 115–127.Google Scholar
[3] Duren, P. L., Theory of Hp Spaces. Pure and Applied Mathematics 38, Academic Press, New York, 1970. Reprint, Dover 2000.Google Scholar
[4] Duren, P. L. and Schuster, A. P., Bergman Spaces. Mathematical Surveys and Monographs 100, American Mathematical Society, Providence, RI, 2004.Google Scholar
[5] Girela, D., Peláez, J. A. and Vukotić, D., Integrability of the derivative of a Blaschke product. Proc. Edinburgh Math. Soc., to appear. http://webpersonal.uma.es/∼GIRELA/danielgirela.htm.Google Scholar
[6] Hedenmalm, H., Korenblum, B., and Zhu, K., Theory of Bergman Spaces. Graduate Texts in Mathematics 199, Springer-Verlag, New York, 2000.Google Scholar
[7] Kim, H. O., Derivatives of Blaschke products. Pacific J. Math. 114(1984), no. 1, 175–190.Google Scholar
[8] Li, K. I., Interpolating Blaschke products and the left spectrum of multiplication operators on the Bergman space. Hokkaido Math. J. 21(1992), no. 2, 295–304.Google Scholar
[9] Vinogradov, S. A., Multiplication and division in the space of analytic functions with area integrable derivative, and in some related spaces. (Russian), Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 222(1995), Issled. po Linein. Oper. i Teor. Funktsii 23, 45–77, 308; translation in J. Math. Sci. (New York) 87(1997), no. 5, 3806–3827.Google Scholar