Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Haukkanen, Pentti
1994.
Roots of Sequences Under Covolutions.
The Fibonacci Quarterly,
Vol. 32,
Issue. 4,
p.
369.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
99.


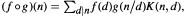 where
where 