Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:15:38.785Z Has data issue: false hasContentIssue false
  • English
  • Français

On Sets of Arcs Containing No Cycles in a Tournament*

Published online by Cambridge University Press:  20 November 2018

K.B. Reid
K.B. Reid*
Affiliation:
University of Illinois, Urbana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A tournament Tn with n nodes is a complete asymmetric digraph [2]. A set S of arcs of a tournament is called consistent if the tournament contains no oriented cycles composed entirely of arcs of S [1]. The object of this note is to provide a new lower bound for f(n), the greatest integer k such that every tournament with n nodes contains a set of k consistent arcs. Erdös and Moon [1] showed that 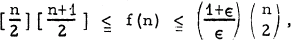where [x] denotes the largest integer not exceeding x, and the second inequality holds for any fixed ∈ > 0 and all sufficiently large n.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 3 , June 1969 , pp. 261 - 264
Copyright
Copyright © Canadian Mathematical Society 1969

Footnotes

*

T Partial support for this paper was received by Office of Naval Research Contract N00014-67A 0305 0008.

References

1. Erdös, P. and Moon, J. W., On sets of consistent arcs in a tournament. Can. Math. Bull. 8 (1965) 269–271.Google Scholar
2. Harary, F., Norman, R. Z. and Cartwright, D., Structural models: An introduction to the theory of directed graphs. (New York, John Wiley and Sons, 1965).Google Scholar
3. Kendall, M.G. and Smith, B. B., On the method of paired comparisons. Biometrika 31 (1939) 324–345.Google Scholar
4. Reid, K.B. and Parker, E. T., Disproof of a conjecture of Erdös and Moser on tournaments. J. Combinatorial Theory (to appear).Google Scholar
5. Reid, K.B., Structure infinite graphs. Ph.D. Thesis, University of Illinois, 1968.Google Scholar