Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T07:20:12.417Z Has data issue: false hasContentIssue false
  • English
  • Français

On Newton's Method and Rational Approximations to Quadratic Irrationals

Published online by Cambridge University Press:  20 November 2018

Edward B. Burger
Edward B. Burger*
Affiliation:
Department of Mathematics Williams College Williamstown, Massachusetts 01267-2606 USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1988 Rieger exhibited a differentiable function having a zero at the golden ratio 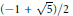$(-1\,+\,\sqrt{5})/2$ for which when Newton's method for approximating roots is applied with an initial value 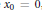${{x}_{0}}\,=\,0$, all approximates are so-called “best rational approximates”—in this case, of the form 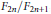${{F}_{2n}}/{{F}_{2n+1}}$, where 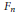${{F}_{n}}$ denotes the 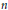$n$-th Fibonacci number. Recently this observation was extended by Komatsu to the class of all quadratic irrationals whose continued fraction expansions have period length 2. Here we generalize these observations by producing an analogous result for all quadratic irrationals and thus provide an explanation for these phenomena.

Keywords

11A5511B37
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 1 , 01 March 2004 , pp. 12 - 16
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Burger, E. B., Exploring the Number Jungle: A Journey into Diophantine Analysis. Amer.Math. Soc., Student Mathematical Library Series, Providence, (2000).Google Scholar
[2] Komatsu, T., Continued fractions and Newton's approximations. Math. Commun. 4 (1999), 167–176.Google Scholar
[3] Komatsu, T., Continued fractions and Newton's approximations, II. Fibonacci Quart. 39 (2001), 336–338.Google Scholar
[4] Rieger, G. J., The golden section and Newton's approximation. Amer.Math. Soc. Abstracts 9(1988), 88T-11-244.Google Scholar
[5] Rieger, G. J., The golden section and Newton's approximation. Fibonacci Quart. 37 (1999), 178–179.Google Scholar
[6] van der Poorten, A. J., An introduction to continued fractions. In: Diophantine Analysis, (eds., J. H. Loxton and A. J. van der Poorten), LondonMath. Soc. Lecture Note Series 109, Cambridge University Press, (1986), 99–138.Google Scholar