Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T17:01:07.959Z Has data issue: false hasContentIssue false
  • English
  • Français

On Lagrangian Catenoids

Published online by Cambridge University Press:  20 November 2018

David E. Blair
David E. Blair*
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824, U. S. A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently I. Castro and F.Urbano introduced the Lagrangian catenoid. Topologically, it is 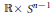$\mathbb{R}\times {{S}^{n-1}}$ and its induced metric is conformally flat, but not cylindrical. Their result is that if a Lagrangian minimal submanifold in 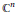${{\mathbb{C}}^{n}}$ is foliated by round $\left( n-1 \right)$-spheres, it is congruent to a Lagrangian catenoid. Here we study the question of conformally flat, minimal, Lagrangian submanifolds in 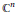${{\mathbb{C}}^{n}}$. The general problem is formidable, but we first show that such a submanifold resembles a Lagrangian catenoid in that its Schouten tensor has an eigenvalue of multiplicity one. Then, restricting to the case of at most two eigenvalues, we show that the submanifold is either flat and totally geodesic or is homothetic to (a piece of) the Lagrangian catenoid.

Keywords

53C4253D12
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 321 - 333
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Blair, D. E., On a generalization of the catenoid. Canad. J. Math. 27(1975), 231–236.Google Scholar
[2] Cartan, É., La déformation des hypersurfaces dans l’espace conforme réel a n ≥ 5 dimensions. Bull. Soc. Math. France 45(1917), 57–121.Google Scholar
[3] Castro, I., The Lagrangian version of a theorem of J. B. Meusnier. In: Summer School on Differential Geometry, Dep. de Matemática, Universidade de Coimbra, 1999, pp. 83–89.Google Scholar
[4] Castro, I. and Urbano, F., On a minimal Lagrangian submanifold of C n foliated by spheres. Michigan Math. J. 46(1999), no. 1, 71–82.Google Scholar
[5] Chen, B.-Y. and Verstraelen, L., A characterization of totally quasiumbilical submanifolds and its applications. Boll. Un. Mat. Ital. 14(1977), 49–57.Google Scholar
[6] Chen, B.-Y. and Yano, K., Sous-variétés localement conformes à un espace euclidien. C. R. Acad. Sci. Paris Sér. A-B 275(1972), 123–126.Google Scholar
[7] Derdziński, A., Some remarks on the local structure of Codazzi tensors. In: Global differential geometry and global analysis, Lecture Notes in Mathematics 838, Springer-Verlag, Berlin, 1981, pp. 251–255.Google Scholar
[8] Ejiri, N., Totally real minimal immersions of n-dimensional real space forms into n-dimensional complex space forms. Proc. Amer. Math. Soc. 84(1982), 243–246.Google Scholar
[9] Harvey, R. and Lawson, H. B., Calibrated geometries. Acta Math. 148(1982), 47–157.Google Scholar
[10] Jagy, W. C., Minimal hypersurfaces foliated by spheres. Michigan Math. J. 38(1991), no. 2, 255–270.Google Scholar
[11] Meusnier, J. B.,Mémoire sur la courbure des surfaces. Mémoires Math. Phys. 10(1785), 477–510.Google Scholar
[12] Moore, J. D. and Morvan, J. M., Sous-variétés conformément plates de codimension quatre. C. R. Acad. Sci. Paris Sér. A-B 287(1978), no. 8, A655–A657.Google Scholar