On Identities with Composition of Generalized Derivations

Abstract

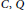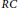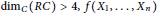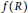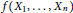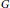Let $R$ be a prime ring with extended centroid $\text{C,Q}$ maximal right ring of quotients of $R$, $RC$ central closure of $R$ such that ${{\dim}_{C}}(RC)>4,f({{X}_{1}},...,{{X}_{n}})$ a multilinear polynomial over $C$ that is not central-valued on $R$, and $f(R)$ the set of all evaluations of the multilinear polynomial $f({{X}_{1}},...,{{X}_{n}})$ in $R$. Suppose that $G$ is a nonzero generalized derivation of $R$ such that 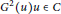${{G}^{2}}(u)u\in C$ for all 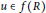$u\in f(R)$. Then one of the following conditions holds:

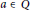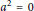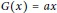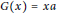• (i) there exists $a\in \text{Q}$ such that ${{a}^{2}}=0$ and either $G(x)=ax$ for all $x\in R$or $G(x)=xa$ for all $x\in R$;

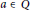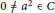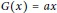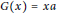• (ii) there exists $a\in \text{Q}$ such that $0\ne {{a}^{2}}\in C$ and either $G(x)=ax$ for all $x\in R$ or $G(x)=xa$ for all $x\in R$ and 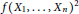$f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$is central-valued on $R$;

• (iii) char 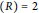$(R)=2$ and one of the following holds:

• (a) there exist 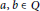$a,b,\in \text{Q}$ such that 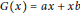$G(x)=ax+xb$ for all $x\in R$ and 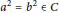${{a}^{2}}={{b}^{2}}\in C$;

• (b) there exist 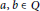$a,b,\in \text{Q}$ such that 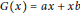$G(x)=ax+xb$ for all 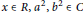$x\in R,\,{{a}^{2}},{{b}^{2}}\in C$ and 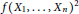$f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on $R$;

• (c) there exist 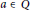$a\in \text{Q}$ and an $X$-outer derivation $d$ of $R$ such that 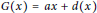$G(x)=ax+d(x)$ for all 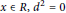$x\in R,{{d}^{2}}=0$ and 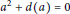${{a}^{2}}+d(a)=0$;

• (d) there exist 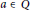$a\in \text{Q}$ and an $X$-outer derivation $d$ of $R$ such that 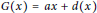$G(x)=ax+d(x)$ for all 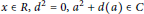$x\in R,\,{{d}^{2}}=0,\,{{a}^{2}}+d(a)\in C$ and 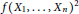$f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on $R$.

Moreover, we characterize the form of nonzero generalized derivations 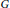$G$ of $R$ satisfying 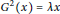${{G}^{2}}(x)=\lambda x$ for all $x\in R$, where 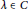$\lambda \in C$.