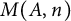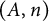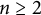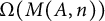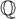1 Introduction
In group theory, if we consider only nilpotent groups, the nilpotency class is the one which measures a distance from commutativity. Already Whitehead [Reference Whitehead21] had the insight that the (J.H.C.) Whitehead products satisfy identities which reflect commutator identities for groups. Berstein and Ganea [Reference Berstein and Ganea3] adapted the nilpotency to H-spaces as follows. Let X be an H-space,
![]() $\varphi _{X,1}=\text {id}_X$
and
$\varphi _{X,1}=\text {id}_X$
and
![]() $\varphi _{X,2} : X^2\to X$
the commutator map. Put
$\varphi _{X,2} : X^2\to X$
the commutator map. Put
![]() $\varphi _{X,n+1} = \varphi _{X,1}\circ (\text {id}_X \times \varphi _{X,n})$
for
$\varphi _{X,n+1} = \varphi _{X,1}\circ (\text {id}_X \times \varphi _{X,n})$
for
![]() $(n+1)$
-fold commutator map of X with
$(n+1)$
-fold commutator map of X with
![]() $n\ge 2$
. An H-space X is called homotopy nilpotent of class n if
$n\ge 2$
. An H-space X is called homotopy nilpotent of class n if
![]() $\varphi _{X,n+1}\simeq \ast $
, is null homotopic but
$\varphi _{X,n+1}\simeq \ast $
, is null homotopic but
![]() $\varphi _{X,n}$
is not [Reference Berstein and Ganea3]. In this case, we write
$\varphi _{X,n}$
is not [Reference Berstein and Ganea3]. In this case, we write
![]() $\text {nil}\,X = n$
.
$\text {nil}\,X = n$
.
Then, Berstein and Ganea [Reference Berstein and Ganea3] introduced a concept of the homotopy nilpotency of a pointed space by means of its loop space. In particular, the m-iterated Samelson products vanish in the loop space
![]() $\Omega (X)$
, or equivalently, the m-iterated Whitehead products vanish in X provided
$\Omega (X)$
, or equivalently, the m-iterated Whitehead products vanish in X provided
![]() $m>\text {nil}\,\Omega (X)$
. We refer to [Reference Whitehead22, Chapter X] for details on Samelson and Whitehead products.
$m>\text {nil}\,\Omega (X)$
. We refer to [Reference Whitehead22, Chapter X] for details on Samelson and Whitehead products.
The homotopy nilpotency classes
![]() $\text {nil}\,X$
of associative H-spaces X has been extensively studied as well as their homotopy commutativity. Work of Hopkins [Reference Hopkins12] drew renewed attention to such problems by relating this classical nilpotency notion with the nilpotence theorem of Devinatz et al. [Reference Devinatz, Hopkins and Smith5]. In particular, Hopkins [Reference Hopkins12] made substantial progress by giving cohomological criteria for homotopy associative finite H-spaces to be homotopy nilpotent. For example, he showed that if a homotopy associative finite H-space has no torsion in the integral homology, then it is homotopy nilpotent. Later, Rao [Reference Rao16] showed that the converse of the above criterion is true in the case of groups
$\text {nil}\,X$
of associative H-spaces X has been extensively studied as well as their homotopy commutativity. Work of Hopkins [Reference Hopkins12] drew renewed attention to such problems by relating this classical nilpotency notion with the nilpotence theorem of Devinatz et al. [Reference Devinatz, Hopkins and Smith5]. In particular, Hopkins [Reference Hopkins12] made substantial progress by giving cohomological criteria for homotopy associative finite H-spaces to be homotopy nilpotent. For example, he showed that if a homotopy associative finite H-space has no torsion in the integral homology, then it is homotopy nilpotent. Later, Rao [Reference Rao16] showed that the converse of the above criterion is true in the case of groups
![]() $\text {Spin}(n)$
and
$\text {Spin}(n)$
and
![]() $SO(n)$
. Eventually, Yagita [Reference Yagita23] proved that, when G is a compact, simply connected Lie group, its p-localization
$SO(n)$
. Eventually, Yagita [Reference Yagita23] proved that, when G is a compact, simply connected Lie group, its p-localization
![]() $G_{(p)}$
is homotopy nilpotent if and only if G has no torsion in the integral homology. Finally, Rao [Reference Rao17] showed that a connected compact Lie group is homotopy nilpotent if and only if it has no torsion in homology.
$G_{(p)}$
is homotopy nilpotent if and only if G has no torsion in the integral homology. Finally, Rao [Reference Rao17] showed that a connected compact Lie group is homotopy nilpotent if and only if it has no torsion in homology.
Although many results on the homotopy nilpotency have been obtained, the homotopy nilpotency classes have been determined in very few cases. It is well-known that for the loop space
![]() $\Omega (\mathbb {S}^m)$
of the m-sphere
$\Omega (\mathbb {S}^m)$
of the m-sphere
![]() $\mathbb {S}^m$
, we have
$\mathbb {S}^m$
, we have
![]() $\text {nil}\,\Omega (\mathbb {S}^m)=1$
if and only if
$\text {nil}\,\Omega (\mathbb {S}^m)=1$
if and only if
![]() $m=1,3,7$
and
$m=1,3,7$
and
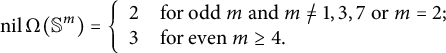 $$ \begin{align*} \mathrm{nil}\,\Omega(\mathbb{S}^m) = \left\{\begin{array}{ll} 2&\text{for odd } m \text{ and } m\not=1,3,7 \text{ or } m = 2;\\ 3&\text{for even } m\ge 4. \end{array}\right. \end{align*} $$
$$ \begin{align*} \mathrm{nil}\,\Omega(\mathbb{S}^m) = \left\{\begin{array}{ll} 2&\text{for odd } m \text{ and } m\not=1,3,7 \text{ or } m = 2;\\ 3&\text{for even } m\ge 4. \end{array}\right. \end{align*} $$
Write
![]() $\mathbb {K}P^m$
for the projective m-space for
$\mathbb {K}P^m$
for the projective m-space for
![]() $\mathbb {K}=\mathbb {R},\,\mathbb {C}$
, the field of reals or complex numbers and
$\mathbb {K}=\mathbb {R},\,\mathbb {C}$
, the field of reals or complex numbers and
![]() $\mathbb {H}$
, the skew
$\mathbb {H}$
, the skew
![]() $\mathbb {R}$
-algebra of quaternions. Then, the homotopy nilpotency of
$\mathbb {R}$
-algebra of quaternions. Then, the homotopy nilpotency of
![]() $\Omega (\mathbb {K}P^m)$
has been first studied by Ganea [Reference Ganea8], Snaith [Reference Snaith19], and then their p-localization
$\Omega (\mathbb {K}P^m)$
has been first studied by Ganea [Reference Ganea8], Snaith [Reference Snaith19], and then their p-localization
![]() $\Omega ((\mathbb {K}P^m)_{(p)})$
by Meier [Reference Meier13]. The homotopy nilpotency of the loop spaces of Grassmann and Stiefel manifolds, and their p-localization have been extensively studied in [Reference Golasiński9].
$\Omega ((\mathbb {K}P^m)_{(p)})$
by Meier [Reference Meier13]. The homotopy nilpotency of the loop spaces of Grassmann and Stiefel manifolds, and their p-localization have been extensively studied in [Reference Golasiński9].
Let
![]() $\mathbb {S}^{2m-1}_{(p)}$
be the p-localization of the sphere
$\mathbb {S}^{2m-1}_{(p)}$
be the p-localization of the sphere
![]() $\mathbb {S}^{2m-1}$
at a prime p. The main result of the paper [Reference Golasiński10] is the explicit determination of the homotopy nilpotence class of a wide range of homotopy associative multiplications on localized spheres
$\mathbb {S}^{2m-1}$
at a prime p. The main result of the paper [Reference Golasiński10] is the explicit determination of the homotopy nilpotence class of a wide range of homotopy associative multiplications on localized spheres
![]() $\mathbb {S}^{2m-1}_{(p)}$
for
$\mathbb {S}^{2m-1}_{(p)}$
for
![]() $p>3$
.
$p>3$
.
The paper grew out of our desire to develop techniques in the study of the homotopy nilpotency classes
![]() $\text {nil}\,\Omega (M(A,n))$
for Moore spaces
$\text {nil}\,\Omega (M(A,n))$
for Moore spaces
![]() $M(A,n)$
with
$M(A,n)$
with
![]() $n\ge 1$
. In Section 1, we set stages for developments to come. This introductory section is devoted to a general discussion and establishes notations on the homotopy nilpotency of H-spaces used in the rest of the paper.
$n\ge 1$
. In Section 1, we set stages for developments to come. This introductory section is devoted to a general discussion and establishes notations on the homotopy nilpotency of H-spaces used in the rest of the paper.
Section 2, takes up the systematic study of the homotopy nilpotency of
![]() $\Omega (M(A,n))$
for
$\Omega (M(A,n))$
for
![]() $n\ge 1$
. First, given a space X, we consider the iterated Samelson product
$n\ge 1$
. First, given a space X, we consider the iterated Samelson product
![]() $s_k : X^{\wedge k}\longrightarrow \Omega \Sigma (X)$
to show in Proposition 3.2 that the space
$s_k : X^{\wedge k}\longrightarrow \Omega \Sigma (X)$
to show in Proposition 3.2 that the space
![]() $\Omega \Sigma (X)$
is not homotopy nilpotent provided the homology
$\Omega \Sigma (X)$
is not homotopy nilpotent provided the homology
![]() $\tilde {H}_{\ast }(X, \mathbb {F})$
has at least two primitive generators, where
$\tilde {H}_{\ast }(X, \mathbb {F})$
has at least two primitive generators, where
![]() $\mathbb {F}$
is a field. Then, we state the main result
$\mathbb {F}$
is a field. Then, we state the main result
Theorem 3.8 If
![]() $M(A,n)$
is a Moore space with
$M(A,n)$
is a Moore space with
![]() $n\ge 2$
then
$n\ge 2$
then
if and only if A is a torsion-free group with rank
![]() $r(A) = 1$
or equivalently, A is a subgroup of
$r(A) = 1$
or equivalently, A is a subgroup of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Unfortunately, Moore spaces of type
![]() $(A,1)$
are not determined uniquely (up to homotopy) by an Abelian group A. At the end, we present constructions and analyse the homotopy nilpotency of some loop spaces
$(A,1)$
are not determined uniquely (up to homotopy) by an Abelian group A. At the end, we present constructions and analyse the homotopy nilpotency of some loop spaces
![]() $\Omega (M(A,1))$
.
$\Omega (M(A,1))$
.
2 Prerequisites
All spaces and maps in this note are assumed to be connected and based with the homotopy type of
![]() $CW$
-complexes unless we assume otherwise. We also do not distinguish notationally between a continuous map and its homotopy class. We write
$CW$
-complexes unless we assume otherwise. We also do not distinguish notationally between a continuous map and its homotopy class. We write
![]() $\Omega (X)$
(resp.
$\Omega (X)$
(resp.
![]() $\Sigma (X)$
) for the loop (resp. suspension) space on a space X and
$\Sigma (X)$
) for the loop (resp. suspension) space on a space X and
![]() $[X,Y]$
for the set of homotopy classes of maps
$[X,Y]$
for the set of homotopy classes of maps
![]() $X\to Y$
.
$X\to Y$
.
Given a space X, we use the customary notations
![]() $X\vee X$
and
$X\vee X$
and
![]() $X\wedge X$
for the wedge and the smash square of X, respectively.
$X\wedge X$
for the wedge and the smash square of X, respectively.
Recall that an H-space is a pair
![]() $(X,\mu )$
, where X is a space and
$(X,\mu )$
, where X is a space and
![]() $\mu : X \times X \to X$
is a map such that the diagram
$\mu : X \times X \to X$
is a map such that the diagram
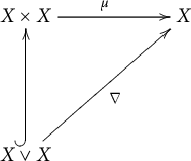
commutes up to homotopy, where
![]() $\nabla : X\vee X\to X$
is the folding map. We call
$\nabla : X\vee X\to X$
is the folding map. We call
![]() $\mu $
a multiplication or an H-structure for X. Two examples of H-spaces come in mind: topological groups and the loop spaces
$\mu $
a multiplication or an H-structure for X. Two examples of H-spaces come in mind: topological groups and the loop spaces
![]() $\Omega (X)$
. In the sequel, we identify an H-space
$\Omega (X)$
. In the sequel, we identify an H-space
![]() $(X,\mu )$
with the space X.
$(X,\mu )$
with the space X.
An H-space X is called a group-like space if X satisfies all the axioms of groups up to homotopy. Recall that a homotopy associative H–
![]() $CW$
-complex always has a homotopy inverse. More precisely, according to [Reference Zabrodsky24, 1.3.2. Corollary] (see also [Reference Arkowitz1, Proposition 8.4.4]), we have
$CW$
-complex always has a homotopy inverse. More precisely, according to [Reference Zabrodsky24, 1.3.2. Corollary] (see also [Reference Arkowitz1, Proposition 8.4.4]), we have
Proposition 2.1 If X is a homotopy associative H–
![]() $CW$
-complex then X is a group-like space.
$CW$
-complex then X is a group-like space.
From now on, we assume that any H-space X is group-like.
Given spaces
![]() $X_1,\ldots ,X_n$
, we use the customary notations
$X_1,\ldots ,X_n$
, we use the customary notations
![]() $X_1\times \cdots \times X_n$
for their Cartesian and
$X_1\times \cdots \times X_n$
for their Cartesian and
![]() $T_m(X_1,\ldots ,X_n)$
for the subspace of
$T_m(X_1,\ldots ,X_n)$
for the subspace of
![]() $X_1\times \cdots \times X_n$
consisting of those points with at least m coordinates at base points with
$X_1\times \cdots \times X_n$
consisting of those points with at least m coordinates at base points with
![]() $m=0,1,\ldots ,n$
. Then,
$m=0,1,\ldots ,n$
. Then,
![]() $T_0(X_1,\ldots ,X_n)= X_1\times \cdots \times X_n$
,
$T_0(X_1,\ldots ,X_n)= X_1\times \cdots \times X_n$
,
![]() $T_1(X_1,\ldots ,X_n)$
is the so called the fat wedge of spaces
$T_1(X_1,\ldots ,X_n)$
is the so called the fat wedge of spaces
![]() $X_1,\ldots ,X_n$
and
$X_1,\ldots ,X_n$
and
![]() $T_{n-1}(X_1,\ldots ,X_n)=X_1\vee \cdots \vee X_n$
, the wedge products of spaces
$T_{n-1}(X_1,\ldots ,X_n)=X_1\vee \cdots \vee X_n$
, the wedge products of spaces
![]() $X_1,\ldots ,X_n$
. We write
$X_1,\ldots ,X_n$
. We write
![]() $j_m(X_1,\ldots ,X_n) : T_m(X_1,\ldots ,X_n)\to X_1\times \cdots \times X_n$
for the inclusion map with
$j_m(X_1,\ldots ,X_n) : T_m(X_1,\ldots ,X_n)\to X_1\times \cdots \times X_n$
for the inclusion map with
![]() $m=0,1,\ldots ,n$
and
$m=0,1,\ldots ,n$
and
![]() $X_1\wedge \cdots \wedge X_n= X_1\times \cdots \times X_n/T_1(X_1,\ldots ,X_n)$
for the smash product of spaces
$X_1\wedge \cdots \wedge X_n= X_1\times \cdots \times X_n/T_1(X_1,\ldots ,X_n)$
for the smash product of spaces
![]() $X_1,\ldots ,X_n$
.
$X_1,\ldots ,X_n$
.
Let
![]() $f_m: (X_m,\star _m)\to (Y_m,\ast _m)$
be continuous maps of pointed topological spaces for
$f_m: (X_m,\star _m)\to (Y_m,\ast _m)$
be continuous maps of pointed topological spaces for
![]() $m=1,\ldots ,n$
. The map
$m=1,\ldots ,n$
. The map
![]() $f_1\times \cdots \times f_n : (X_1\times \cdots \times X_n, (\star _1,\ldots ,\star _n))\to (Y_1\times \cdots \times Y_n,(\ast _1,\ldots ,\ast _n))$
sends the point
$f_1\times \cdots \times f_n : (X_1\times \cdots \times X_n, (\star _1,\ldots ,\star _n))\to (Y_1\times \cdots \times Y_n,(\ast _1,\ldots ,\ast _n))$
sends the point
![]() $(x_1,\ldots ,x_n)$
into
$(x_1,\ldots ,x_n)$
into
![]() $(f_1(x_1),\ldots , f_n(x_n))$
for
$(f_1(x_1),\ldots , f_n(x_n))$
for
![]() $(x_1,\ldots ,x_n)\in X_1\times \cdots \times X_n$
and restricts to maps
$(x_1,\ldots ,x_n)\in X_1\times \cdots \times X_n$
and restricts to maps
![]() $T_m(f_1,\ldots ,f_n) : T_m(X_1,\ldots , X_n)\to T_m(Y_1,\ldots ,Y_n)$
with
$T_m(f_1,\ldots ,f_n) : T_m(X_1,\ldots , X_n)\to T_m(Y_1,\ldots ,Y_n)$
with
![]() $m=0,1,\ldots ,n$
. If
$m=0,1,\ldots ,n$
. If
![]() $X_m=X$
and
$X_m=X$
and
![]() $f_m=f$
for
$f_m=f$
for
![]() $m=1,\ldots ,n$
then we write
$m=1,\ldots ,n$
then we write
![]() $X^n=X_1\times \cdots \times X_n$
,
$X^n=X_1\times \cdots \times X_n$
,
![]() $X^{\wedge n}=X_1\wedge \cdots \wedge X_n$
,
$X^{\wedge n}=X_1\wedge \cdots \wedge X_n$
,
![]() $f^n=f_1\times \cdots \times f_n$
and
$f^n=f_1\times \cdots \times f_n$
and
![]() $f^{\wedge n}=f_1\wedge \cdots \wedge f_n$
. The identity map of a space X involved is consistently denoted by
$f^{\wedge n}=f_1\wedge \cdots \wedge f_n$
. The identity map of a space X involved is consistently denoted by
![]() $\iota _X$
.
$\iota _X$
.
Given an H-group X, the functor
![]() $[ -, X]$
takes its values in the category of groups. One may then ask when those functors take their values in various subcategories of groups. For example, X is homotopy commutative if and only if
$[ -, X]$
takes its values in the category of groups. One may then ask when those functors take their values in various subcategories of groups. For example, X is homotopy commutative if and only if
![]() $[Y, X]$
is Abelian for all Y.
$[Y, X]$
is Abelian for all Y.
Given an H-space X, we write
![]() $\varphi _{X,1}=\iota _X$
,
$\varphi _{X,1}=\iota _X$
,
![]() $\varphi _{X,2}: X^2\to X$
for the basic commutator map and
$\varphi _{X,2}: X^2\to X$
for the basic commutator map and
![]() $\varphi _{X,n+1}=\varphi _{X,2}\circ (\varphi _{X,n}\times \iota _X)$
for
$\varphi _{X,n+1}=\varphi _{X,2}\circ (\varphi _{X,n}\times \iota _X)$
for
![]() $n\ge 2$
.
$n\ge 2$
.
2.1 The nilpotency class
The nilpotency class
![]() $\mathrm{nil}\, (X,\mu )$
of an H-space
$\mathrm{nil}\, (X,\mu )$
of an H-space
![]() $(X,\mu )$
is the least integer
$(X,\mu )$
is the least integer
![]() $n\ge 0$
for which the map
$n\ge 0$
for which the map
![]() $\varphi _{X,n+1}\simeq \ast $
is nullhomotopic and we call the homotopy associative H-space X homotopy nilpotent. If no such integer exists, we put
$\varphi _{X,n+1}\simeq \ast $
is nullhomotopic and we call the homotopy associative H-space X homotopy nilpotent. If no such integer exists, we put
![]() $\mathrm{nil}\,(X,\mu )=\infty $
. In the sequel, we simply write
$\mathrm{nil}\,(X,\mu )=\infty $
. In the sequel, we simply write
![]() $\mathrm{nil}\, X$
for the nilpotency class of an H-space X. Thus,
$\mathrm{nil}\, X$
for the nilpotency class of an H-space X. Thus,
![]() $\mathrm{nil}\, X=0$
if and only if X is contractible and, as is easily seen,
$\mathrm{nil}\, X=0$
if and only if X is contractible and, as is easily seen,
![]() $\mathrm{nil}\, X\le 1$
if and only if X is homotopy commutative.
$\mathrm{nil}\, X\le 1$
if and only if X is homotopy commutative.
The set
![]() $\pi _0(X)$
of all path-components of an H-space X is known to be a group. The following result is easy to prove:
$\pi _0(X)$
of all path-components of an H-space X is known to be a group. The following result is easy to prove:
Lemma 2.2 If X is an H-space and the path component of the base-point
![]() $\star \in X$
is contractible then
$\star \in X$
is contractible then
![]() $\mathrm{nil} \pi _0(X) = \mathrm{nil}\,X.$
$\mathrm{nil} \pi _0(X) = \mathrm{nil}\,X.$
The definition of the nilpotency classes may be extended to maps. The nilpotency class
![]() $\mathrm{nil}\, f$
of an H-map
$\mathrm{nil}\, f$
of an H-map
![]() $f: X_1\to X_2$
is the least integer
$f: X_1\to X_2$
is the least integer
![]() $n\ge 0$
for which the map
$n\ge 0$
for which the map
![]() $f\circ \varphi _{X,n+1} : X_1^{n+1}\to X_2$
is nullhomotopic; if no such integer exists, we put
$f\circ \varphi _{X,n+1} : X_1^{n+1}\to X_2$
is nullhomotopic; if no such integer exists, we put
![]() $\mathrm{nil}\, f=\infty $
.
$\mathrm{nil}\, f=\infty $
.
In the sequel, we need
Lemma 2.3 If X is an H-space then the composite map
is nullhomotopic.
Since the space
![]() $X^{\wedge n}$
, the nth smash power of X is the homotopy cofiber of the map
$X^{\wedge n}$
, the nth smash power of X is the homotopy cofiber of the map
![]() $j_1(X,\ldots ,X) : T_1(X,\ldots ,X)\to X^n$
, the result above implies an existence of a map
$j_1(X,\ldots ,X) : T_1(X,\ldots ,X)\to X^n$
, the result above implies an existence of a map
![]() $\bar {\varphi }_{X,n} : X^{\wedge n}\to X$
for
$\bar {\varphi }_{X,n} : X^{\wedge n}\to X$
for
![]() $n\ge 1$
with
$n\ge 1$
with
![]() $\bar {\varphi }_{X,1}=\varphi _{X,1}$
.
$\bar {\varphi }_{X,1}=\varphi _{X,1}$
.
It is well known that the quotient map
![]() $X^n \to X^{\wedge n}$
has a right homotopy inverse after suspending for
$X^n \to X^{\wedge n}$
has a right homotopy inverse after suspending for
![]() $n\ge 1$
, and the fact that X is an H-space means that the suspension map
$n\ge 1$
, and the fact that X is an H-space means that the suspension map
![]() $[Y,X] \to [\Sigma Y,\Sigma X]$
is a monomorphism for any space Y. Thus, we may state
$[Y,X] \to [\Sigma Y,\Sigma X]$
is a monomorphism for any space Y. Thus, we may state
Proposition 2.4 Let X be an H-space. Then
![]() $\varphi _{X,n}\simeq \ast $
if and only if
$\varphi _{X,n}\simeq \ast $
if and only if
![]() $\bar {\varphi }_{X,n}\simeq \ast $
for
$\bar {\varphi }_{X,n}\simeq \ast $
for
![]() $n\ge 1$
.
$n\ge 1$
.
Then, [Reference Berstein and Ganea3, 2.7. Theorem] and Proposition 2.4 lead to
Theorem 2.5 If X is an H-space then
where m ranges over all integers and Y over all topological spaces.
Furthermore, in view of [Reference Zabrodsky24, Lemma 2.6.1], we may state
Corollary 2.6 A connected H-space X is homotopy nilpotent if and only if the functor
![]() $[- , X]$
on the category of all spaces is nilpotent group valued.
$[- , X]$
on the category of all spaces is nilpotent group valued.
Proof Certainly, the homotopy nilpotency of a connected associative H-space X implies that the functor
![]() $[- , X]$
on the category of all pointed spaces is nilpotent group valued.
$[- , X]$
on the category of all pointed spaces is nilpotent group valued.
Now, suppose that the functor
![]() $[-, X]$
is nilpotent groups valued and
$[-, X]$
is nilpotent groups valued and
![]() $\mathrm{nil}\,[\prod _1^{\infty } X, X] < n$
. Then, for the projection map
$\mathrm{nil}\,[\prod _1^{\infty } X, X] < n$
. Then, for the projection map
![]() $\prod _1^{\infty } X\to X^n$
on the first n factors, the composite map
$\prod _1^{\infty } X\to X^n$
on the first n factors, the composite map
is null-homotopic. Since, the projection
![]() $\prod _1^{\infty } X\to X^n$
has a retraction, we deduce that the map
$\prod _1^{\infty } X\to X^n$
has a retraction, we deduce that the map
![]() $\varphi _{X,n} : X^n\to X$
is also null-homotopic and the proof is complete.▪
$\varphi _{X,n} : X^n\to X$
is also null-homotopic and the proof is complete.▪
Next, notice that for a map
![]() $f : X\to Y$
of H-spaces, we have the commutative (up to homotopy) diagram
$f : X\to Y$
of H-spaces, we have the commutative (up to homotopy) diagram
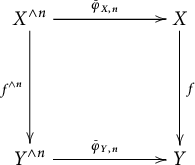
with
![]() $n\ge 1$
.
$n\ge 1$
.
This yields
Remark 2.7 If
![]() $X'$
is an H-subspace of an H-space X and
$X'$
is an H-subspace of an H-space X and
![]() $r: X\to X'$
its a homotopy H-retract then one can easily derive from the above that
$r: X\to X'$
its a homotopy H-retract then one can easily derive from the above that
2.2 Homotopy nilpotency of spaces
With any based space X, we associate the integer
![]() $\mathrm{nil}\,\Omega (X)$
called the nilpotency class of X. Evidently,
$\mathrm{nil}\,\Omega (X)$
called the nilpotency class of X. Evidently,
![]() $\mathrm{nil}\,\pi _1(X)\le \mathrm{nil}\, \Omega (X)$
. We give an extension of this result involving Whitehead products, generally denoted by
$\mathrm{nil}\,\pi _1(X)\le \mathrm{nil}\, \Omega (X)$
. We give an extension of this result involving Whitehead products, generally denoted by
![]() $[\alpha _1,\alpha _2]\in \pi _{m_1+m_2-1}(X)$
if
$[\alpha _1,\alpha _2]\in \pi _{m_1+m_2-1}(X)$
if
![]() $\alpha _i\in \pi _{m_i}(X)$
for
$\alpha _i\in \pi _{m_i}(X)$
for
![]() $m_i\ge 1$
with
$m_i\ge 1$
with
![]() $i=1,2$
.
$i=1,2$
.
We define
![]() $(n+1)$
-fold Whitehead products
$(n+1)$
-fold Whitehead products
![]() $[\alpha _1,\ldots ,\alpha _{n+1}]$
as
$[\alpha _1,\ldots ,\alpha _{n+1}]$
as
![]() $[[\alpha _1,\ldots ,\alpha _n],\alpha _{n+1}]$
if
$[[\alpha _1,\ldots ,\alpha _n],\alpha _{n+1}]$
if
![]() $\alpha _i\in \pi _{m_i}(X)$
for
$\alpha _i\in \pi _{m_i}(X)$
for
![]() $m_i\ge 1$
with
$m_i\ge 1$
with
![]() $i=1,\ldots ,n+1$
agreeing that, for
$i=1,\ldots ,n+1$
agreeing that, for
![]() $n=0$
,
$n=0$
,
![]() $[\alpha ]=\alpha $
.
$[\alpha ]=\alpha $
.
Recall that
![]() $\text {W-length}\,X$
, the Whitehead length of a space X is the least integer
$\text {W-length}\,X$
, the Whitehead length of a space X is the least integer
![]() $n\ge 0$
such that
$n\ge 0$
such that
![]() $[\alpha _1,\ldots ,\alpha _{n+1}]=0$
for all
$[\alpha _1,\ldots ,\alpha _{n+1}]=0$
for all
![]() $\alpha _i\in \pi _{m_i}(X)$
,
$\alpha _i\in \pi _{m_i}(X)$
,
![]() $m_i\ge 1$
; if no such integer exists, we put
$m_i\ge 1$
; if no such integer exists, we put
![]() $\text {W-length}\,X=\infty $
.
$\text {W-length}\,X=\infty $
.
Then, according to [Reference Berstein and Ganea3, Reference Bott and Samelson4.Reference Dror6. Theorem], we by have:
Theorem 2.8
![]() $\text {W-length}\,X\le \mathrm{nil}\,\Omega (X).$
$\text {W-length}\,X\le \mathrm{nil}\,\Omega (X).$
Example 2.9 (1) It is well-known that
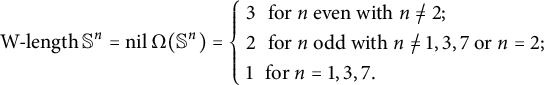 $$ \begin{align*} \text{W-length}\,\mathbb{S}^n=\mathrm{nil}\,\Omega(\mathbb{S}^n)=\begin{cases} ~3\, ~\text{ for } n \text{ even with } n\not=2;\\ ~2\, ~\text{ for } n \text{ odd with } n\not=1,3,7 \text{ or } n=2;\\ ~1\, ~\text{ for } n=1,3,7. \end{cases} \end{align*} $$
$$ \begin{align*} \text{W-length}\,\mathbb{S}^n=\mathrm{nil}\,\Omega(\mathbb{S}^n)=\begin{cases} ~3\, ~\text{ for } n \text{ even with } n\not=2;\\ ~2\, ~\text{ for } n \text{ odd with } n\not=1,3,7 \text{ or } n=2;\\ ~1\, ~\text{ for } n=1,3,7. \end{cases} \end{align*} $$
(2) For the wedge
![]() $\mathbb {S}^m\vee \mathbb {S}^n$
of two spheres with
$\mathbb {S}^m\vee \mathbb {S}^n$
of two spheres with
![]() $m,n\ge 2$
, there is an iterated nontrivial Whitehead product of any length. Therefore, by Theorem 2.8, we conclude that
$m,n\ge 2$
, there is an iterated nontrivial Whitehead product of any length. Therefore, by Theorem 2.8, we conclude that
The concept of a nilpotent space is due to Dror [Reference Dror6]. Recall that a pointed path-connected space X is said to be nilpotent if its fundamental group
![]() $\pi _1(X)$
acts nilpotently on the higher homotopy groups
$\pi _1(X)$
acts nilpotently on the higher homotopy groups
![]() $\pi _n(X)$
for
$\pi _n(X)$
for
![]() $n\ge 1$
. Since, the action of
$n\ge 1$
. Since, the action of
![]() $\pi _1(X)$
on
$\pi _1(X)$
on
![]() $\pi _n(X)$
for
$\pi _n(X)$
for
![]() $n\ge 1$
may be written in terms of Whitehead products, the nilpotency of a space X is a lower bound of its homotopy nilpotency
$n\ge 1$
may be written in terms of Whitehead products, the nilpotency of a space X is a lower bound of its homotopy nilpotency
![]() $\mathrm{nil}\,\Omega (X)$
. Therefore, by Theorem 2.8, the space X is nilpotent if
$\mathrm{nil}\,\Omega (X)$
. Therefore, by Theorem 2.8, the space X is nilpotent if
![]() $\Omega (X)$
is homotopy nilpotent. But, by Example 2.9(2), not every space
$\Omega (X)$
is homotopy nilpotent. But, by Example 2.9(2), not every space
![]() $\Omega (X)$
is homotopy nilpotent if X is nilpotent or even simply connected.
$\Omega (X)$
is homotopy nilpotent if X is nilpotent or even simply connected.
Dror [Reference Dror6] has also published a far-reaching generalization of a classical theorem of J.H.C. Whitehead useful in the next section.
Theorem 2.11 If
![]() $f: X\to Y$
is a map of connected, pointed,
$f: X\to Y$
is a map of connected, pointed,
![]() $CW$
-complexes which induces an isomorphism on integral homology, and if X and Y are nilpotent spaces, then f is a homotopy equivalence.
$CW$
-complexes which induces an isomorphism on integral homology, and if X and Y are nilpotent spaces, then f is a homotopy equivalence.
3 Moore spaces
We take up the systematic study of the homotopy nilpotency of Moore spaces
![]() $M(A,n)$
for
$M(A,n)$
for
![]() $n\ge 1$
. In Eckmann–Hilton duality, Moore spaces play the role of dual objects of Eilenberg–MacLane
$n\ge 1$
. In Eckmann–Hilton duality, Moore spaces play the role of dual objects of Eilenberg–MacLane
![]() $CW$
-complexes.
$CW$
-complexes.
Let A be an Abelian group and n any integer
![]() $\ge 1$
. A
$\ge 1$
. A
![]() $CW$
-complex X (if one such exists) satisfying
$CW$
-complex X (if one such exists) satisfying
![]() $\pi _j(X) = 0$
for
$\pi _j(X) = 0$
for
![]() $j < n$
,
$j < n$
,
![]() $\pi _n(X)\approx A$
and
$\pi _n(X)\approx A$
and
![]() $H_i(X)=0$
for
$H_i(X)=0$
for
![]() $i> n$
is known as a Moore space of type
$i> n$
is known as a Moore space of type
![]() $(A, n)$
, or simply an
$(A, n)$
, or simply an
![]() $M(A, n)$
space. By [Reference Moore15], it is known that a Moore space
$M(A, n)$
space. By [Reference Moore15], it is known that a Moore space
![]() $M(A,n)$
with
$M(A,n)$
with
![]() $n\ge 2$
exists and, in view of [Reference Hatcher11, Example 4.34], the homotopy type of a Moore space
$n\ge 2$
exists and, in view of [Reference Hatcher11, Example 4.34], the homotopy type of a Moore space
![]() $M(A,n)$
is uniquely determined by A and
$M(A,n)$
is uniquely determined by A and
![]() $n\ge 2$
. This implies that every Moore space
$n\ge 2$
. This implies that every Moore space
![]() $M(A,n)$
with
$M(A,n)$
with
![]() $n\ge 3$
, is the suspension
$n\ge 3$
, is the suspension
![]() $\Sigma M(A,n-1)$
. Furthermore, in [Reference Arkowitz and Golasiński2, Section 2], it was shown that also
$\Sigma M(A,n-1)$
. Furthermore, in [Reference Arkowitz and Golasiński2, Section 2], it was shown that also
![]() $M(A,2)$
is a suspension
$M(A,2)$
is a suspension
![]() $\Sigma L(A)$
for some
$\Sigma L(A)$
for some
![]() $CW$
-complex
$CW$
-complex
![]() $L(A)$
.
$L(A)$
.
By means of [Reference Varadarajan20, Proposition 1.1], there exists an
![]() $M(A,1)$
space if and only if the homology
$M(A,1)$
space if and only if the homology
![]() $H_2(A,\mathbb {Z})=0$
for the ring
$H_2(A,\mathbb {Z})=0$
for the ring
![]() $\mathbb {Z}$
of integers. Recall also that, by [Reference Miller14, Theorem 3],
$\mathbb {Z}$
of integers. Recall also that, by [Reference Miller14, Theorem 3],
![]() $H_2(A,\mathbb {Z})=0$
if and only if
$H_2(A,\mathbb {Z})=0$
if and only if
![]() $A\otimes A$
coincides with its subgroup generated by the diagonal,
$A\otimes A$
coincides with its subgroup generated by the diagonal,
![]() $\{a\otimes a;\,a\in A \}$
.
$\{a\otimes a;\,a\in A \}$
.
Remark 3.1 If
![]() $X_1,X_2$
are Moore spaces of type
$X_1,X_2$
are Moore spaces of type
![]() $(A,1)$
then, like for Moore spaces of type
$(A,1)$
then, like for Moore spaces of type
![]() $(A,n)$
with
$(A,n)$
with
![]() $n \ge 2$
, there is an integral homotopy isomorphism
$n \ge 2$
, there is an integral homotopy isomorphism
![]() $f : X_1\to X_2$
. If the spaces
$f : X_1\to X_2$
. If the spaces
![]() $X_1,X_2$
are nilpotent then Theorem 2.11 implies that
$X_1,X_2$
are nilpotent then Theorem 2.11 implies that
![]() $f : X_1 \to X_2$
is a homotopy equivalence.
$f : X_1 \to X_2$
is a homotopy equivalence.
However, the homotopy type of a Moore space
![]() $M(A,1)$
is not uniquely determined by A. Hatcher [Reference Hatcher11, Example 4.35] constructed the space
$M(A,1)$
is not uniquely determined by A. Hatcher [Reference Hatcher11, Example 4.35] constructed the space
![]() $X=(\mathbb {S}^1\vee \mathbb {S}^n)\cup e^{n+1}$
such that the inclusion
$X=(\mathbb {S}^1\vee \mathbb {S}^n)\cup e^{n+1}$
such that the inclusion
![]() $\mathbb {S}^1 \hookrightarrow X$
induces an isomorphism on all homology groups and on
$\mathbb {S}^1 \hookrightarrow X$
induces an isomorphism on all homology groups and on
![]() $\pi _k$
for
$\pi _k$
for
![]() $k < n$
, but not on
$k < n$
, but not on
![]() $\pi _n$
. More precisely, from [Reference Hatcher11, Example 4.27] we have
$\pi _n$
. More precisely, from [Reference Hatcher11, Example 4.27] we have
![]() $\pi _n(\mathbb {S}^1\vee \mathbb {S}^n)\approx \mathbb {Z}[t,t^{-1}]/(2t-1)$
. Then, X is obtained from
$\pi _n(\mathbb {S}^1\vee \mathbb {S}^n)\approx \mathbb {Z}[t,t^{-1}]/(2t-1)$
. Then, X is obtained from
![]() $\mathbb {S}^1\vee \mathbb {S}^n$
by attaching a cell
$\mathbb {S}^1\vee \mathbb {S}^n$
by attaching a cell
![]() $e^{n+1}$
via a map
$e^{n+1}$
via a map
![]() $\mathbb {S}^n\to \mathbb {S}^1\vee \mathbb {S}^n$
corresponding to
$\mathbb {S}^n\to \mathbb {S}^1\vee \mathbb {S}^n$
corresponding to
![]() $2t-1\in \mathbb {Z}[t,t^{-1}]$
.
$2t-1\in \mathbb {Z}[t,t^{-1}]$
.
3.1 Moore spaces of type
 $\mathbf {(A,n)}$
with
$\mathbf {(A,n)}$
with
 $\mathbf {n}\ge \mathbf {2}$
$\mathbf {n}\ge \mathbf {2}$
To examine the homotopy nilpotency of
![]() $M(A,n)$
with
$M(A,n)$
with
![]() $\ge 2$
, we need to fix some notations and recall a definition. Given a pointed space X, write
$\ge 2$
, we need to fix some notations and recall a definition. Given a pointed space X, write
![]() $i_1,i_2 : X\to X\times X$
for the canonical embedding maps and
$i_1,i_2 : X\to X\times X$
for the canonical embedding maps and
![]() $\Delta : X\to X\times X$
for the diagonal map. If
$\Delta : X\to X\times X$
for the diagonal map. If
![]() $H_m(X,A)$
is the mth homology group of X with coefficient in an Abelian group A then an element
$H_m(X,A)$
is the mth homology group of X with coefficient in an Abelian group A then an element
![]() $\alpha \in H_m(X,A)$
is said to be primitive if
$\alpha \in H_m(X,A)$
is said to be primitive if
![]() $\Delta _{\ast }(\alpha )=i_{1\ast }(\alpha )+ i_{2\ast }(\alpha )$
for the induced homomorphisms
$\Delta _{\ast }(\alpha )=i_{1\ast }(\alpha )+ i_{2\ast }(\alpha )$
for the induced homomorphisms
![]() $i_{1 \ast },i_{2 \ast }, \Delta _{\ast } : H_m(X,A)\to H_m(X\times X,A)$
.
$i_{1 \ast },i_{2 \ast }, \Delta _{\ast } : H_m(X,A)\to H_m(X\times X,A)$
.
We show that the space
![]() $\Omega \Sigma (X)$
is not homotopy nilpotent provided the homology
$\Omega \Sigma (X)$
is not homotopy nilpotent provided the homology
![]() $H_{\ast }(X, \mathbb {F})$
has at least two primitive generators, where
$H_{\ast }(X, \mathbb {F})$
has at least two primitive generators, where
![]() $\mathbb {F}$
is a field.
$\mathbb {F}$
is a field.
Proposition 3.2 If
![]() $\tilde {H}_{\ast }(X, \mathbb {F})$
has at least two primitive generators, where
$\tilde {H}_{\ast }(X, \mathbb {F})$
has at least two primitive generators, where
![]() $\mathbb {F}$
is a field then
$\mathbb {F}$
is a field then
![]() $\Omega \Sigma (X)$
is not homotopy nilpotent.
$\Omega \Sigma (X)$
is not homotopy nilpotent.
Proof To see this, take homology
![]() $H_{\ast }(X,\mathbb {F})$
with
$H_{\ast }(X,\mathbb {F})$
with
![]() $\mathbb {F}$
-coefficients and recall that the Bott–Samelson Theorem [Reference Bott and Samelson4] states that
$\mathbb {F}$
-coefficients and recall that the Bott–Samelson Theorem [Reference Bott and Samelson4] states that
![]() $H_{\ast }(\Omega \Sigma X,\mathbb {F})\approx T(\tilde {H}_{\ast }(X,\mathbb {F}))$
, the tensor algebra on
$H_{\ast }(\Omega \Sigma X,\mathbb {F})\approx T(\tilde {H}_{\ast }(X,\mathbb {F}))$
, the tensor algebra on
![]() $\tilde {H}_{\ast }(X,\mathbb {F})$
. This may be rewritten as
$\tilde {H}_{\ast }(X,\mathbb {F})$
. This may be rewritten as
![]() $UL\big <\tilde {H}_{\ast }(X,\mathbb {F})\big>$
, where
$UL\big <\tilde {H}_{\ast }(X,\mathbb {F})\big>$
, where
![]() $L\big <\tilde {H}_{\ast }(X,\mathbb {F})\big>$
is the free Lie algebra generated by
$L\big <\tilde {H}_{\ast }(X,\mathbb {F})\big>$
is the free Lie algebra generated by
![]() $\tilde {H}_{\ast }(X,\mathbb {F})$
and
$\tilde {H}_{\ast }(X,\mathbb {F})$
and
![]() $UL\big <\tilde {H}_{\ast }(X,\mathbb {F})\big>$
is its universal enveloping algebra. Further, the suspension
$UL\big <\tilde {H}_{\ast }(X,\mathbb {F})\big>$
is its universal enveloping algebra. Further, the suspension
![]() $E : X \to \Omega \Sigma X$
induces the inclusion of the generating set in homology. Now, consider the iterated Samelson product
$E : X \to \Omega \Sigma X$
induces the inclusion of the generating set in homology. Now, consider the iterated Samelson product
where
![]() $s_1=E$
,
$s_1=E$
,
![]() $s_{k+1}=\big < E,s_k\big>$
, the Samelson product of
$s_{k+1}=\big < E,s_k\big>$
, the Samelson product of
![]() $s_k$
and E for
$s_k$
and E for
![]() $n\ge 2$
. For any
$n\ge 2$
. For any
![]() $x\in \tilde {H}_{\ast }(X)$
we have
$x\in \tilde {H}_{\ast }(X)$
we have
![]() $E_{\ast }(x) = x$
.
$E_{\ast }(x) = x$
.
The effect of the Samelson product map on homology classes of loop spaces is presented e.g., in [Reference Whitehead22, Chapter X, Section 6] (see also [Reference Hatcher11, Chapter 3]). If
![]() $x_1,\ldots ,x_k\in \tilde {H}_{\ast }(X,\mathbb {F})$
are primitive then the class
$x_1,\ldots ,x_k\in \tilde {H}_{\ast }(X,\mathbb {F})$
are primitive then the class
![]() $x_1\otimes \cdots \otimes x_k\in \tilde {H}_{\ast } (X,\mathbb {F})^{\otimes k}\approx \tilde {H}_{\ast }(X^{\wedge k},\mathbb {F})$
is sent by
$x_1\otimes \cdots \otimes x_k\in \tilde {H}_{\ast } (X,\mathbb {F})^{\otimes k}\approx \tilde {H}_{\ast }(X^{\wedge k},\mathbb {F})$
is sent by
![]() $(s_k)_{\ast }$
to the iterated bracket
$(s_k)_{\ast }$
to the iterated bracket
![]() $[x_1, [x_2,\ldots [x_{k-1},x_k]]\ldots ]$
. In particular, if
$[x_1, [x_2,\ldots [x_{k-1},x_k]]\ldots ]$
. In particular, if
![]() $x,y\in \tilde {H}_{\ast }(X,\mathbb {F})$
are distinct primitive generators then the class
$x,y\in \tilde {H}_{\ast }(X,\mathbb {F})$
are distinct primitive generators then the class
is in the image of
![]() $(s_k)_{\ast }$
. Hence,
$(s_k)_{\ast }$
. Hence,
![]() $s_k$
cannot be null homotopic.
$s_k$
cannot be null homotopic.
Notice that for the map
![]() $s_k : X^{\wedge k}\longrightarrow \Omega \Sigma (X)$
defined above, there is by the factorization
$s_k : X^{\wedge k}\longrightarrow \Omega \Sigma (X)$
defined above, there is by the factorization
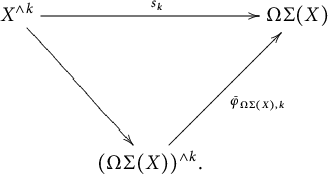
Consequently, the map
![]() $\bar {\varphi }_{\Omega \Sigma X,k}$
is not null homotopic provided the map
$\bar {\varphi }_{\Omega \Sigma X,k}$
is not null homotopic provided the map
![]() $s_k$
is so and the proof is complete.▪
$s_k$
is so and the proof is complete.▪
To apply Proposition 3.2 for computations of
![]() $\mathrm{nil}\,\Omega M(A,n)$
, we need
$\mathrm{nil}\,\Omega M(A,n)$
, we need
Lemma 3.3 If
![]() $n\ge 2$
then
$n\ge 2$
then
for
![]() $m=1,2,\ldots \infty $
and
$m=1,2,\ldots \infty $
and
![]() $n\ge 2$
.
$n\ge 2$
.
Proof Given an Abelian group A, write
![]() $X_n(A)=M(A,n)$
with
$X_n(A)=M(A,n)$
with
![]() $n\ge 2$
or
$n\ge 2$
or
![]() $X_1(A)=L(A)$
. Then, by the Universal Coefficient Theorem, we have
$X_1(A)=L(A)$
. Then, by the Universal Coefficient Theorem, we have
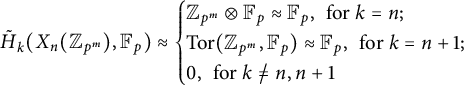 $$ \begin{align*} \tilde{H}_k(X_n(\mathbb{Z}_{p^m}),\mathbb{F}_p)\approx \begin{cases}\mathbb{Z}_{p^m}\otimes \mathbb{F}_p\approx\mathbb{F}_p ,\,\text{ for } k = n;\\ \text{Tor}(\mathbb{Z}_{p^m}, \mathbb{F}_p)\approx\mathbb{F}_p,\,\text{ for } k = n +1;\\ 0,\,\text{ for } k\not=n,n+1\end{cases} \end{align*} $$
$$ \begin{align*} \tilde{H}_k(X_n(\mathbb{Z}_{p^m}),\mathbb{F}_p)\approx \begin{cases}\mathbb{Z}_{p^m}\otimes \mathbb{F}_p\approx\mathbb{F}_p ,\,\text{ for } k = n;\\ \text{Tor}(\mathbb{Z}_{p^m}, \mathbb{F}_p)\approx\mathbb{F}_p,\,\text{ for } k = n +1;\\ 0,\,\text{ for } k\not=n,n+1\end{cases} \end{align*} $$
for
![]() $m,n\ge 1$
.
$m,n\ge 1$
.
Since the Moore space
![]() $M(\mathbb {Z}_{p^m},n)\simeq \Sigma X_{n-1}(\mathbb {Z}_{p^m})$
for
$M(\mathbb {Z}_{p^m},n)\simeq \Sigma X_{n-1}(\mathbb {Z}_{p^m})$
for
![]() $n\ge 2$
, we can consider the iterated Samelson product
$n\ge 2$
, we can consider the iterated Samelson product
Thus, Proposition 3.2 implies that
for
![]() $m\ge 1$
and
$m\ge 1$
and
![]() $n\ge 2$
.
$n\ge 2$
.
Because
![]() $\mathbb {Z}_{p^{\infty }}\otimes \mathbb {F}_p=0$
, we have
$\mathbb {Z}_{p^{\infty }}\otimes \mathbb {F}_p=0$
, we have
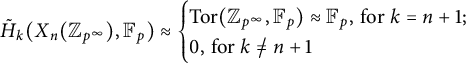 $$ \begin{align*} \tilde{H}_k(X_n(\mathbb{Z}_{p^{\infty}}),\mathbb{F}_p)\approx \begin{cases} \text{Tor}(\mathbb{Z}_{p^{\infty}}, \mathbb{F}_p)\approx\mathbb{F}_p,\,\text{for } k=n+1;\\ 0,\,\text{for } k\not=n+1 \end{cases} \end{align*} $$
$$ \begin{align*} \tilde{H}_k(X_n(\mathbb{Z}_{p^{\infty}}),\mathbb{F}_p)\approx \begin{cases} \text{Tor}(\mathbb{Z}_{p^{\infty}}, \mathbb{F}_p)\approx\mathbb{F}_p,\,\text{for } k=n+1;\\ 0,\,\text{for } k\not=n+1 \end{cases} \end{align*} $$
for
![]() $n\ge 1$
. Thus, the argument above collapses.
$n\ge 1$
. Thus, the argument above collapses.
Therefore, we process as follows. Given
![]() $n\ge 2$
and a prime p, consider the mapping telescope T determined by the sequence of maps
$n\ge 2$
and a prime p, consider the mapping telescope T determined by the sequence of maps
Recall that T is the union of the mapping cylinders
![]() $M_k$
with the copies of
$M_k$
with the copies of
![]() $\mathbb {S}^n$
in
$\mathbb {S}^n$
in
![]() $M_k$
and
$M_k$
and
![]() $M_{k-1}$
identified for all k. Thus, T is the quotient space of the disjoint union
$M_{k-1}$
identified for all k. Thus, T is the quotient space of the disjoint union
![]() $\bigsqcup _{k=1}^{\infty } \mathbb {S}^n\times [k,k+1]$
in which each point
$\bigsqcup _{k=1}^{\infty } \mathbb {S}^n\times [k,k+1]$
in which each point
![]() $(x_k,k+1)\in \mathbb {S}^n\times [k,k+1]$
is identified with
$(x_k,k+1)\in \mathbb {S}^n\times [k,k+1]$
is identified with
![]() $(p(x_k),k+1)\in \mathbb{S}^n\times [k+1,k+2]$
. In the mapping telescope T, let
$(p(x_k),k+1)\in \mathbb{S}^n\times [k+1,k+2]$
. In the mapping telescope T, let
![]() $T_m$
be the union of the first m mapping cylinders. This deformation retracts onto
$T_m$
be the union of the first m mapping cylinders. This deformation retracts onto
![]() $\mathbb {S}^n$
by deformation retracting each mapping cylinder onto its right end in turn. Since the maps
$\mathbb {S}^n$
by deformation retracting each mapping cylinder onto its right end in turn. Since the maps
![]() $p: \mathbb {S}^n\to \mathbb {S}^n$
are cellular, each mapping cylinder is a
$p: \mathbb {S}^n\to \mathbb {S}^n$
are cellular, each mapping cylinder is a
![]() $CW$
-complex and the telescope T is the increasing union of the subcomplexes
$CW$
-complex and the telescope T is the increasing union of the subcomplexes
![]() $T_m\simeq \mathbb {S}^n$
.
$T_m\simeq \mathbb {S}^n$
.
If we attach a cell
![]() $e^{n+1}$
to the first
$e^{n+1}$
to the first
![]() $\mathbb {S}^n$
in T via the identity map of
$\mathbb {S}^n$
in T via the identity map of
![]() $\mathbb {S}^n$
, we obtain a space X which is the increasing union of its subspaces
$\mathbb {S}^n$
, we obtain a space X which is the increasing union of its subspaces
![]() $X_m=T_m\cup e^{n+1}$
being
$X_m=T_m\cup e^{n+1}$
being
![]() $M(\mathbb {Z}_{p^m},n)$
’s. Since,
$M(\mathbb {Z}_{p^m},n)$
’s. Since,
![]() $H_n(X,\mathbb {Z})\approx \text {colim}_mH_n(X_m,\mathbb {Z})=\text {colim}_m\mathbb {Z}_{p^m}=\mathbb {Z}_{p^{\infty }}$
and
$H_n(X,\mathbb {Z})\approx \text {colim}_mH_n(X_m,\mathbb {Z})=\text {colim}_m\mathbb {Z}_{p^m}=\mathbb {Z}_{p^{\infty }}$
and
![]() $H_k(X,\mathbb {Z})=0$
for
$H_k(X,\mathbb {Z})=0$
for
![]() $k\not =n$
, we derive that X is the Moore space of type
$k\not =n$
, we derive that X is the Moore space of type
![]() $(\mathbb {Z}_{p^{\infty }},n)$
.
$(\mathbb {Z}_{p^{\infty }},n)$
.
Furthermore,
![]() $\Omega (X)=\text {colim}_m\Omega (X_m)$
implies a homotopy equivalence
$\Omega (X)=\text {colim}_m\Omega (X_m)$
implies a homotopy equivalence
Thus, the nontrivial maps
for
![]() $k,m\ge 1$
determined by (3.1) yield the nontrivial the maps
$k,m\ge 1$
determined by (3.1) yield the nontrivial the maps
for
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $n\ge 2$
. Consequently,
$n\ge 2$
. Consequently,
for
![]() $n\ge 2$
and this concludes the proof.▪
$n\ge 2$
and this concludes the proof.▪
Now, recall that by [Reference Fuchs7, Corollary 27.4], an Abelian group A with elements of finite order contains a direct summand
![]() $\mathbb {Z}_{p^m}$
for some prime p and
$\mathbb {Z}_{p^m}$
for some prime p and
![]() $m=1,2,\ldots $
or
$m=1,2,\ldots $
or
![]() $\infty $
. Then, such an Abelian group
$\infty $
. Then, such an Abelian group
![]() $A\approx \mathbb {Z}_{p^m}\oplus B$
for some Abelian group B and
$A\approx \mathbb {Z}_{p^m}\oplus B$
for some Abelian group B and
![]() $m=1,\ldots ,\infty $
.
$m=1,\ldots ,\infty $
.
Hence,
![]() $M(A,n)=M(\mathbb {Z}_{p^m},n)\vee M(B,n)$
and so Remark 2.7, and Lemma 3.3 imply that
$M(A,n)=M(\mathbb {Z}_{p^m},n)\vee M(B,n)$
and so Remark 2.7, and Lemma 3.3 imply that
for
![]() $n\ge 2$
.
$n\ge 2$
.
Given an Abelian group A, we have
![]() $A\otimes \mathbb {Q}=\bigoplus _1^{{\tiny r}(A)}\mathbb {Q}$
for the rank
$A\otimes \mathbb {Q}=\bigoplus _1^{{\tiny r}(A)}\mathbb {Q}$
for the rank
![]() $r(A)$
of A and the additive group
$r(A)$
of A and the additive group
![]() $\mathbb {Q}$
of the field
$\mathbb {Q}$
of the field
![]() $\mathbb {Q}$
of rationals. Therefore,
$\mathbb {Q}$
of rationals. Therefore,
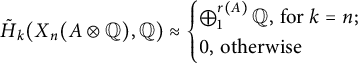 $$ \begin{align*} \tilde{H}_k(X_n(A\otimes\mathbb{Q}),\mathbb{Q})\approx \begin{cases}\bigoplus_1^{r(A)}\mathbb{Q},\,\text{for } k = n;\\ 0,\,\text{otherwise} \end{cases}\end{align*} $$
$$ \begin{align*} \tilde{H}_k(X_n(A\otimes\mathbb{Q}),\mathbb{Q})\approx \begin{cases}\bigoplus_1^{r(A)}\mathbb{Q},\,\text{for } k = n;\\ 0,\,\text{otherwise} \end{cases}\end{align*} $$
for
![]() $n\ge 1$
.
$n\ge 1$
.
Next, by for a nilpotent space X and a set of primes I, write
![]() $X_{(I)}$
for the I-localization of X. Then, by [Reference Meier13, Proposition 3.5], we have
$X_{(I)}$
for the I-localization of X. Then, by [Reference Meier13, Proposition 3.5], we have
Proposition 3.6 Let X be a nilpotent space. If
![]() $\mathrm{nil}\, \Omega (X) < n$
then
$\mathrm{nil}\, \Omega (X) < n$
then
![]() $\mathrm{nil}\,\Omega (X_{(I)}) < n$
for every set of primes I.
$\mathrm{nil}\,\Omega (X_{(I)}) < n$
for every set of primes I.
Since the Moore space
![]() $M(A,n)\simeq \Sigma X_{n-1}(A)$
for
$M(A,n)\simeq \Sigma X_{n-1}(A)$
for
![]() $n\ge 2$
, we can consider the iterated Samelson product
$n\ge 2$
, we can consider the iterated Samelson product
Furthermore, if
![]() $r(A)\ge 2$
then Proposition 3.2 yields
$r(A)\ge 2$
then Proposition 3.2 yields
![]() $\mathrm{nil}\,\Omega (M(A\otimes \mathbb {Q},n))=\infty $
. Since
$\mathrm{nil}\,\Omega (M(A\otimes \mathbb {Q},n))=\infty $
. Since
![]() $M(A\otimes \mathbb {Q},n)=M(A,n)_{(0)}$
, the rationalization of
$M(A\otimes \mathbb {Q},n)=M(A,n)_{(0)}$
, the rationalization of
![]() $M(A,n)$
, Proposition 3.6 leads to
$M(A,n)$
, Proposition 3.6 leads to
![]() $\mathrm{nil}\,\Omega (M(A,n))=\infty $
. Thus, in view of Proposition 3.2 and Lemma 3.3, we may state
$\mathrm{nil}\,\Omega (M(A,n))=\infty $
. Thus, in view of Proposition 3.2 and Lemma 3.3, we may state
Corollary 3.7 If A is an Abelian group with elements of finite order or
![]() $r(A)\ge 2$
then
$r(A)\ge 2$
then
for
![]() $n\ge 2$
.
$n\ge 2$
.
If
![]() $r(A)=1$
and A is a torsion-free Abelian group then by [Reference Fuchs7, Chapter IV, Section 24], we know that A is a subgroup of
$r(A)=1$
and A is a torsion-free Abelian group then by [Reference Fuchs7, Chapter IV, Section 24], we know that A is a subgroup of
![]() $\mathbb {Q}$
. Notice that
$\mathbb {Q}$
. Notice that
![]() $M(\mathbb {Q},n)=\mathbb {S}^n_{(0)}=K(\mathbb {Q},n)$
, the Eilenberg–MacLane of type
$M(\mathbb {Q},n)=\mathbb {S}^n_{(0)}=K(\mathbb {Q},n)$
, the Eilenberg–MacLane of type
![]() $(\mathbb {Q},n)$
provided n is odd. Therefore,
$(\mathbb {Q},n)$
provided n is odd. Therefore,
![]() $M(\mathbb {Q},n)$
is a homotopy commutative and associative H-space and
$M(\mathbb {Q},n)$
is a homotopy commutative and associative H-space and
![]() $\mathrm{nil}\,M(\mathbb {Q},n)=\mathrm{nil}\,\Omega (M(\mathbb {Q},n))=~1$
.
$\mathrm{nil}\,M(\mathbb {Q},n)=\mathrm{nil}\,\Omega (M(\mathbb {Q},n))=~1$
.
Given any subgroup
![]() $A< \mathbb {Q}$
, we have a sequence
$A< \mathbb {Q}$
, we have a sequence
![]() $\mathbb {Z}\stackrel {n_0}\to \mathbb {Z}\stackrel {n_1}\to \mathbb {Z}\stackrel {n_2}\to \cdots $
and
$\mathbb {Z}\stackrel {n_0}\to \mathbb {Z}\stackrel {n_1}\to \mathbb {Z}\stackrel {n_2}\to \cdots $
and
![]() $A=\text {colim}_{n_k}\mathbb {Z}$
. Next, for
$A=\text {colim}_{n_k}\mathbb {Z}$
. Next, for
![]() $n\ge 2$
, the mapping telescope T of the associated sequence of maps
$n\ge 2$
, the mapping telescope T of the associated sequence of maps
is the union of the mapping cylinders
![]() $M_{n_k}$
with the copies of
$M_{n_k}$
with the copies of
![]() $\mathbb {S}^n$
in
$\mathbb {S}^n$
in
![]() $M_{n_k}$
and
$M_{n_k}$
and
![]() $M_{n_{k-1}}$
identified for all k. In the mapping telescope T, let
$M_{n_{k-1}}$
identified for all k. In the mapping telescope T, let
![]() $T_m$
be the union of the first m mapping cylinders. This deformation retracts onto
$T_m$
be the union of the first m mapping cylinders. This deformation retracts onto
![]() $\mathbb {S}^n$
by deformation retracting each mapping cylinder onto its right end in turn. Since the maps
$\mathbb {S}^n$
by deformation retracting each mapping cylinder onto its right end in turn. Since the maps
![]() $n_k: \mathbb {S}^n\to \mathbb {S}^n$
are cellular, each mapping cylinder is a
$n_k: \mathbb {S}^n\to \mathbb {S}^n$
are cellular, each mapping cylinder is a
![]() $CW$
-complex and the telescope T is the increasing union of the subcomplexes
$CW$
-complex and the telescope T is the increasing union of the subcomplexes
![]() $T_m\simeq \mathbb {S}^n=M(\mathbb {Z},n)$
. Next, by
$T_m\simeq \mathbb {S}^n=M(\mathbb {Z},n)$
. Next, by
![]() $\tilde {H}_n(T,\mathbb {Z})\approx A=\text {colim}_m\mathbb {Z}$
and
$\tilde {H}_n(T,\mathbb {Z})\approx A=\text {colim}_m\mathbb {Z}$
and
![]() $\tilde {H}_k(T,\mathbb {Z})=0$
for
$\tilde {H}_k(T,\mathbb {Z})=0$
for
![]() $k\not =n$
, we derive that
$k\not =n$
, we derive that
![]() $T=M(A,n)=\text {colim}_mT_m$
. Then,
$T=M(A,n)=\text {colim}_mT_m$
. Then,
![]() $\Omega (M(A,n))= \text {colim}_m\Omega (T_m)$
and
$\Omega (M(A,n))= \text {colim}_m\Omega (T_m)$
and
![]() $\mathrm{nil}\,\Omega (T_m))=\mathrm{nil}\,\Omega (\mathbb {S}^n)\le 3$
imply that
$\mathrm{nil}\,\Omega (T_m))=\mathrm{nil}\,\Omega (\mathbb {S}^n)\le 3$
imply that
![]() $\mathrm{nil}\,\Omega (M(A,n))\le 3$
provided
$\mathrm{nil}\,\Omega (M(A,n))\le 3$
provided
![]() $n\ge 2$
and we get the main result
$n\ge 2$
and we get the main result
Theorem 3.8 If
![]() $M(A,n)$
is a Moore space with
$M(A,n)$
is a Moore space with
![]() $n\ge 2$
then
$n\ge 2$
then
if and only if A is a torsion-free group with rank
![]() $r(A) = 1$
or equivalently, A is a subgroup of
$r(A) = 1$
or equivalently, A is a subgroup of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
3.2 Moore spaces of type
 $\mathbf {(A,1)}$
$\mathbf {(A,1)}$
We present constructions and analyse homotopy nilpotency of some Moore spaces of type
![]() $(A,1)$
.
$(A,1)$
.
(1) The space
![]() $X=(\mathbb {S}^1\vee \mathbb {S}^n)\cup e^{n+1}$
constructed by Hatcher [Reference Hatcher11, Example 4.35] is a Moore space of type
$X=(\mathbb {S}^1\vee \mathbb {S}^n)\cup e^{n+1}$
constructed by Hatcher [Reference Hatcher11, Example 4.35] is a Moore space of type
![]() $(\mathbb {Z},1)$
for the infinite cyclic group
$(\mathbb {Z},1)$
for the infinite cyclic group
![]() $\mathbb {Z}\big < t\big>$
. Since
$\mathbb {Z}\big < t\big>$
. Since
![]() $\pi _1(X)\approx \mathbb {Z}\big < t\big>$
and
$\pi _1(X)\approx \mathbb {Z}\big < t\big>$
and
![]() $\pi _n(\mathbb {S}^1\vee \mathbb {S}^n)\approx \mathbb {Z}[t,t^{-1}]/(2t-1)$
, we get that
$\pi _n(\mathbb {S}^1\vee \mathbb {S}^n)\approx \mathbb {Z}[t,t^{-1}]/(2t-1)$
, we get that
![]() $(2t-1)\alpha =0$
implies
$(2t-1)\alpha =0$
implies
![]() $2t\alpha =\alpha $
for
$2t\alpha =\alpha $
for
![]() $\alpha \in \mathbb {Z}[t,t^{-1}]/(2t-1)$
. Hence, the action of
$\alpha \in \mathbb {Z}[t,t^{-1}]/(2t-1)$
. Hence, the action of
![]() $\pi _1(X)$
on
$\pi _1(X)$
on
![]() $\pi _n(X)$
is nontrivial.
$\pi _n(X)$
is nontrivial.
Note that the map
![]() $\mathbb {Z}[t,t^{-1}]\to \mathbb {Q}$
given by
$\mathbb {Z}[t,t^{-1}]\to \mathbb {Q}$
given by
![]() $t\mapsto 1/2$
yields a ring isomorphism
$t\mapsto 1/2$
yields a ring isomorphism
for the subring
![]() $\mathbb {Z}[1/2]\subseteq \mathbb {Q}$
consisting of rationals with denominator a power of
$\mathbb {Z}[1/2]\subseteq \mathbb {Q}$
consisting of rationals with denominator a power of
![]() $2$
. Then,
$2$
. Then,
![]() $\pi _1(X)\approx \mathbb {Z}\big < t\big > $
acts on
$\pi _1(X)\approx \mathbb {Z}\big < t\big > $
acts on
![]() $\pi _n(X)\approx \mathbb {Z}[1/2]$
by
$\pi _n(X)\approx \mathbb {Z}[1/2]$
by
![]() $t\alpha =(1/2)\alpha $
for
$t\alpha =(1/2)\alpha $
for
![]() $\alpha \in \mathbb {Z}[1/2]$
. Consequently, the Whitehead product
$\alpha \in \mathbb {Z}[1/2]$
. Consequently, the Whitehead product
![]() $[t,\alpha ]=(-1/2)\alpha $
and the
$[t,\alpha ]=(-1/2)\alpha $
and the
![]() $(n+1)$
-fold Whitehead product
$(n+1)$
-fold Whitehead product
![]() $[\alpha ,t,t\ldots ,t]=(-1/2)^n\alpha $
is non-trivial for
$[\alpha ,t,t\ldots ,t]=(-1/2)^n\alpha $
is non-trivial for
![]() $n\ge 1$
provided
$n\ge 1$
provided
![]() $\alpha \not =0$
. Consequently, in view of Theorem 2.8,
$\alpha \not =0$
. Consequently, in view of Theorem 2.8,
(2) The space
![]() $\mathbb {R}P^2_m=\mathbb {S}^1\cup _me^2$
is a Moore space of type
$\mathbb {R}P^2_m=\mathbb {S}^1\cup _me^2$
is a Moore space of type
![]() $(\mathbb {Z}_m,1)$
for the cyclic group
$(\mathbb {Z}_m,1)$
for the cyclic group
![]() $\mathbb {Z}_m$
of order m. Then,
$\mathbb {Z}_m$
of order m. Then,
![]() $\pi _1(\mathbb {R}P^2_m)=\mathbb {Z}_m\big < t\big > $
, where t is represented by the canonical map
$\pi _1(\mathbb {R}P^2_m)=\mathbb {Z}_m\big < t\big > $
, where t is represented by the canonical map
![]() $i : \mathbb {S}^1\to \mathbb {R}P^2_m$
. Next, by [Reference Sieradski18], the group
$i : \mathbb {S}^1\to \mathbb {R}P^2_m$
. Next, by [Reference Sieradski18], the group
![]() $\pi _2(\mathbb {R}P^2_m)$
can be identified with the ideal of the group ring
$\pi _2(\mathbb {R}P^2_m)$
can be identified with the ideal of the group ring
![]() $\mathbb {Z}[\mathbb {Z}_m]$
generated by
$\mathbb {Z}[\mathbb {Z}_m]$
generated by
![]() $\alpha =1-t$
, so that as an Abelian group
$\alpha =1-t$
, so that as an Abelian group
![]() $\pi _2(\mathbb {R}P^2_m)$
is free of rank
$\pi _2(\mathbb {R}P^2_m)$
is free of rank
![]() $m-1$
and, as
$m-1$
and, as
![]() $\pi _1$
-module,
$\pi _1$
-module,
![]() $\pi _2(\mathbb {R}P^2_m)$
has a single generator
$\pi _2(\mathbb {R}P^2_m)$
has a single generator
![]() $\alpha $
, subject solely to the relation
$\alpha $
, subject solely to the relation
![]() $(1+t+\cdots +t^{m-1})\alpha =0$
. Then, the Whitehead product
$(1+t+\cdots +t^{m-1})\alpha =0$
. Then, the Whitehead product
![]() $[\alpha ,t]=t\alpha -\alpha =2\alpha -t^2\alpha -\cdots -t^{m-1}\alpha $
. Thus, we derive that the
$[\alpha ,t]=t\alpha -\alpha =2\alpha -t^2\alpha -\cdots -t^{m-1}\alpha $
. Thus, we derive that the
![]() $(n+1)$
-fold Whitehead product
$(n+1)$
-fold Whitehead product
![]() $[\alpha ,t,t\ldots ,t]$
is non-trivial for
$[\alpha ,t,t\ldots ,t]$
is non-trivial for
![]() $n\ge 1$
. Consequently, in view of Theorem 2.8, we derive that
$n\ge 1$
. Consequently, in view of Theorem 2.8, we derive that
for
![]() $m\ge 2$
.
$m\ge 2$
.
(3) If
![]() $r(A)=1$
and A is a torsion-free Abelian group then
$r(A)=1$
and A is a torsion-free Abelian group then
![]() $A< \mathbb {Q}$
, we have a sequence of maps
$A< \mathbb {Q}$
, we have a sequence of maps
![]() $\mathbb {Z}\stackrel {n_0}\to \mathbb {Z}^n\stackrel {n_1}\to \mathbb {Z}\stackrel {n_2}\to \cdots $
and
$\mathbb {Z}\stackrel {n_0}\to \mathbb {Z}^n\stackrel {n_1}\to \mathbb {Z}\stackrel {n_2}\to \cdots $
and
![]() $A=\text {colim}_{k_i}\mathbb {Z}$
. Next, the mapping telescope T of the associated sequence of maps
$A=\text {colim}_{k_i}\mathbb {Z}$
. Next, the mapping telescope T of the associated sequence of maps
is the union of the mapping cylinders
![]() $M_{n_k}$
with the copies of
$M_{n_k}$
with the copies of
![]() $\mathbb {S}^1$
in
$\mathbb {S}^1$
in
![]() $M_{n_k}$
and
$M_{n_k}$
and
![]() $M_{n_{k-1}}$
identified for all k. In the mapping telescope T, let
$M_{n_{k-1}}$
identified for all k. In the mapping telescope T, let
![]() $T_m$
be the union of the first m mapping cylinders. This deformation retracts onto
$T_m$
be the union of the first m mapping cylinders. This deformation retracts onto
![]() $\mathbb {S}^1$
by deformation retracting each mapping cylinder onto its right end in turn. Since the maps
$\mathbb {S}^1$
by deformation retracting each mapping cylinder onto its right end in turn. Since the maps
![]() $n_k: \mathbb {S}^1\to \mathbb {S}^n$
are cellular, each mapping cylinder is a
$n_k: \mathbb {S}^1\to \mathbb {S}^n$
are cellular, each mapping cylinder is a
![]() $CW$
-complex and the telescope T is the increasing union of the subcomplexes
$CW$
-complex and the telescope T is the increasing union of the subcomplexes
![]() $T_m\simeq \mathbb {S}^1$
.
$T_m\simeq \mathbb {S}^1$
.
Next, by
![]() $\tilde {H}_1(T,\mathbb {Z})\approx \text {colim}_mH_1(T_m)=\text {colim}_{k_i}\mathbb {Z}=A$
and
$\tilde {H}_1(T,\mathbb {Z})\approx \text {colim}_mH_1(T_m)=\text {colim}_{k_i}\mathbb {Z}=A$
and
![]() $\tilde {H}_k(T,\mathbb {Z})=0$
for
$\tilde {H}_k(T,\mathbb {Z})=0$
for
![]() $k\not =1$
, we derive that
$k\not =1$
, we derive that
![]() $T=\text {colim}_mT_m$
is a Moore space of type
$T=\text {colim}_mT_m$
is a Moore space of type
![]() $(A,1)$
. Furthermore,
$(A,1)$
. Furthermore,
![]() $\pi _k(T)=\text {colim}_m\pi _k(T_m)$
implies that
$\pi _k(T)=\text {colim}_m\pi _k(T_m)$
implies that
![]() $\pi _1(T)=\text {colim}_m\mathbb {Z}=A$
and
$\pi _1(T)=\text {colim}_m\mathbb {Z}=A$
and
![]() $\pi _k(T)=0$
for
$\pi _k(T)=0$
for
![]() $k\not = 1$
. Consequently,
$k\not = 1$
. Consequently,
![]() $T=\text {colim}_mT_m$
, as the Eilenberg-MacLane space
$T=\text {colim}_mT_m$
, as the Eilenberg-MacLane space
![]() $K(A,1)$
, is a homotopy commutative and an associative H-space. Finally, we get that
$K(A,1)$
, is a homotopy commutative and an associative H-space. Finally, we get that
(4) At the end, given a prime p, consider the telescope T determined by the sequence of maps
If we attach a cell
![]() $e^2$
to the first
$e^2$
to the first
![]() $\mathbb {S}^1$
in T via the identity map of
$\mathbb {S}^1$
in T via the identity map of
![]() $\mathbb {S}^1$
, we obtain a space X which is a Moore space of type
$\mathbb {S}^1$
, we obtain a space X which is a Moore space of type
![]() $(\mathbb {Z}_{p^{\infty }},1)$
since X is the increasing union of its subspaces
$(\mathbb {Z}_{p^{\infty }},1)$
since X is the increasing union of its subspaces
![]() $X_m=T_m\cup e^2$
, which are
$X_m=T_m\cup e^2$
, which are
![]() $\mathbb {R}P^2_{p^m}$
’s. Then, (2) leads to
$\mathbb {R}P^2_{p^m}$
’s. Then, (2) leads to