Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T14:45:30.594Z Has data issue: false hasContentIssue false
  • English
  • Français

On dual unit balls of Thurston norms

Published online by Cambridge University Press:  07 October 2021

Abdoul Karim Sane
Abdoul Karim Sane*
Affiliation:
Institut Fourier, Université Grenoble Alpes, Grenoble, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

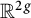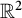Thurston norms are invariants of 3-manifolds defined on their second homology and understanding the shape of their dual unit balls is a widely open problem. In this article, we provide a large family of polytopes in $\mathbb {R}^{2g}$ that appear like dual unit balls of Thurston norms, generalizing Thurston’s construction for polygons in $\mathbb {R}^2$ .

À mes enseignants, premiers

Keywords

Thurston NormIntersection normReebless foliationIncompressible surface
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 674 - 685
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agol, I., Hass, J., and Thurston, W., The computational complexity of knot genus and spanning area. Trans. AMS 358(2006), no. 9, 3821–3850.10.1090/S0002-9947-05-03919-XCrossRefGoogle Scholar
Cossarini, M. and Dehornoy, P., Intersection norms on surfaces and Birkhoff sections for geodesic flows. Preprint, 2021. arXiv:1604.06688 Google Scholar
Gabai, D., Foliations and the topology of 3-manifolds. J. Differ. Geom. 18(1983), 445–503.10.4310/jdg/1214437784CrossRefGoogle Scholar
Hatcher, A., Notes on basic 3-manifold topology. http://pi.math.cornell.edu/hatcher/3M/3Mfds.pdf Google Scholar
Lackenby, M., The efficient certification of knottedness and Thurston norm. Adv. Math. (accepted) arXiv:1604.00290 Google Scholar
Montesinos, J. M., Classical tessellations and three-manifolds. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Sane, A., Intersection norm and one-faced collections. Comp. Rendus Math. 358, no. 8 (2020), 941–956.Google Scholar
Scharlemann, M., Sutured manifolds and generalized Thurston norms. J. Differ. Geom. 29(1989), 557–614.10.4310/jdg/1214443063CrossRefGoogle Scholar
Thurston, W., A norm for the homology of three manifolds. Mem. Amer. Math. Soc. 339(1986), 99–130.Google Scholar
Turaev, V., A norm for the cohomology of 2-complexes. Alg. Geom. Top. 2(2002), 137–155.10.2140/agt.2002.2.137CrossRefGoogle Scholar
Waldhausen, F., Eine Klasse von 3-dimensionaler Mannigfaltigkeiten I. Inventiones 3(1967), 308–333.10.1007/BF01402956CrossRefGoogle Scholar