Article contents
On a Paper by M. Iosifescu and S. Marcus
Published online by Cambridge University Press: 20 November 2018
Extract
In this paper we will construct an example showing that the problem posed in [1] has a negative answer. Two more theorems on the subject treated in [1] will be included.
Let Io = [0, 1], R the reals, and let, for A ⊂ R, Ao be the interior of A. Let {xn} be a sequence in [0, 1> such that 0 = x1 < x2 < … and lim xn = 1. For each n, let In be closed interval having x as its midpoint (except for n = 1 in which case x1 is the left endpoint of I1) such that In ∩ Im= ϕ, and the metric density relative to Io of 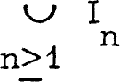 at 1 is zero. Let Jn be a closed interval in In concentric with In (except for n = 1, where J1 has x1 as its left endpoint) whose length is half that of In
at 1 is zero. Let Jn be a closed interval in In concentric with In (except for n = 1, where J1 has x1 as its left endpoint) whose length is half that of In
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1963
References
- 1
- Cited by


