Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Indlekofer, K. -H.
and
Manstavičius, E.
1993.
Functional limit theorems for additive arithmetic functions on intervals.
Lithuanian Mathematical Journal,
Vol. 33,
Issue. 3,
p.
217.


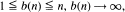 let
let