No CrossRef data available.
Article contents
A Note on the Diophantine Equation x2 + y6 = ze, e ≥ 4
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We consider the diophantine equation 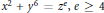 ${{x}^{2}}\,+\,{{y}^{6}}\,=\,{{z}^{e}},\,e\,\le \,4$. We show that, when
${{x}^{2}}\,+\,{{y}^{6}}\,=\,{{z}^{e}},\,e\,\le \,4$. We show that, when  $e$ is a multiple of 4 or 6, this equation has no solutions in positive integers with
$e$ is a multiple of 4 or 6, this equation has no solutions in positive integers with 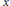 $x$ and
$x$ and  $y$ relatively prime. As a corollary, we show that there exists no primitive Pythagorean triangle one of whose leglengths is a perfect cube, while the hypotenuse length is an integer square.
$y$ relatively prime. As a corollary, we show that there exists no primitive Pythagorean triangle one of whose leglengths is a perfect cube, while the hypotenuse length is an integer square.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
[1] Instructional conference and workshop on diophantine equations. Lorentz Center, Leiden University, The Netherlands. May 7–11, 2007 and May 14–16, 2007.Google Scholar
[2] Sierpinski, W., Elementary theory of numbers. North-Holland Mathematical Library, 31. North-Holland Publishing Co., Amsterdam; PWN—Polish Scientific Publishers, Warsaw, 1988, pp. 73–74, 78–79.Google Scholar
[3] Pocklington, H. C., Some diophantine impossibilities. Proc. Cambridge Philos. Soc.
17(1914), 108–121.Google Scholar
[4] Dickson, L. E., History of the theory of numbers. III. Quadratic and higher forms.
AMS Chelsea Publishing, Providence, RI, 1992,Google Scholar


