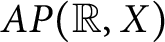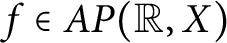1 Introduction
The definition of an almost periodic function given by Bohr in his pioneering work [Reference Bohr6] is based on two properly generalized concepts: the periodicity to the so-called almost periodicity, and the periodic distribution of periods to the so-called relative density of almost periods. Specifically, a continuous function
![]() $f:\mathbb {R}\to \mathbb {C}$
is almost periodic if for every
$f:\mathbb {R}\to \mathbb {C}$
is almost periodic if for every
![]() $\varepsilon>0$
, there corresponds a number
$\varepsilon>0$
, there corresponds a number
![]() $l=l(\varepsilon )>0$
such that each interval of length l contains a number
$l=l(\varepsilon )>0$
such that each interval of length l contains a number
![]() $\tau $
satisfying
$\tau $
satisfying
![]() $|f(t+\tau )-f(t)|<\varepsilon $
for all t. In particular, this notion yields that f is bounded and uniformly continuous. We will denote as
$|f(t+\tau )-f(t)|<\varepsilon $
for all t. In particular, this notion yields that f is bounded and uniformly continuous. We will denote as
![]() $AP(\mathbb {R},\mathbb {C})$
the space of almost periodic functions in the sense of this definition (Bohr’s condition). It is noteworthy that almost periodic functions occur frequently and they are more often encountered in the study of various phenomena than the rather special periodic ones. For example, note that the sum of the two periodic functions of a real variable
$AP(\mathbb {R},\mathbb {C})$
the space of almost periodic functions in the sense of this definition (Bohr’s condition). It is noteworthy that almost periodic functions occur frequently and they are more often encountered in the study of various phenomena than the rather special periodic ones. For example, note that the sum of the two periodic functions of a real variable
![]() $t\mapsto e^{it}$
and
$t\mapsto e^{it}$
and
![]() $t\mapsto e^{i\sqrt {2}t}$
is not periodic, but it is almost periodic.
$t\mapsto e^{i\sqrt {2}t}$
is not periodic, but it is almost periodic.
In the course of time, Bohr’s work was studied by several mathematicians, such as Amerio, Besicovitch, Bochner, Corduneanu, Favard, Fink, Levitan, Lusternik, Pontryagin, Prouse, Stepanov, and Von-Neumann, Weyl, who also contributed to develop and expand this theory completely. Moreover, several variants and extensions of Bohr’s concept were introduced, most notably by Besicovitch, Stepanov, and Weyl. In this context, we can cite, among others, the papers [Reference Amerio and Prouse1–Reference Besicovitch3, Reference Bochner5, Reference Bohr7, Reference Bohr8, Reference Corduneanu10–Reference Lusternik and Sobolevitan15, Reference Stepanov21, Reference von Neumann22] and the references therein.
Without a doubt, almost periodic functions have played an important role in various branches of mathematics since their introduction by Bohr during the 1920s. Indeed, as the literature about this topic shows, this theory has many important applications in problems of ordinary and partial differential equations, dynamical systems, stability theory, nonlinear oscillations theory, and so on, which have at the same time a wide scope of applications in various fields of science and technology. Moreover, the theory of almost periodic functions opened a way to study a wide class of trigonometric series of the general type and even exponential series.
In this paper, we focus our attention on the case when the values taken by such functions belong to a Banach space, which were defined and studied by Bochner in 1933 [Reference Bochner4]. Let
![]() $(X,\|\cdot \|)$
be an arbitrary Banach space over
$(X,\|\cdot \|)$
be an arbitrary Banach space over
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {C}$
, and we shall briefly present the basic properties of
$\mathbb {C}$
, and we shall briefly present the basic properties of
![]() $AP(\mathbb {R},X)$
, which is defined, in terms of Bohr’s property, as the set of continuous functions
$AP(\mathbb {R},X)$
, which is defined, in terms of Bohr’s property, as the set of continuous functions
![]() $f:\mathbb {R}\to X$
such that, fixed
$f:\mathbb {R}\to X$
such that, fixed
![]() $\varepsilon>0$
, there corresponds a relatively dense set
$\varepsilon>0$
, there corresponds a relatively dense set
![]() $\{\tau _j\}$
of real numbers satisfying
$\{\tau _j\}$
of real numbers satisfying
![]() $\|f(t+\tau _j)-f(t)\|<\varepsilon $
for
$\|f(t+\tau _j)-f(t)\|<\varepsilon $
for
![]() $t\in \mathbb {R}$
and
$t\in \mathbb {R}$
and
![]() $\tau _j\in \{\tau _j\}$
. This theory is, in its essential lines, similar to the theory of numerical almost periodic functions. It is plain that all functions f in
$\tau _j\in \{\tau _j\}$
. This theory is, in its essential lines, similar to the theory of numerical almost periodic functions. It is plain that all functions f in
![]() $AP(\mathbb {R},X)$
are bounded and uniformly continuous. Moreover,
$AP(\mathbb {R},X)$
are bounded and uniformly continuous. Moreover,
![]() $AP(\mathbb {R}, X)$
is a Banach space equipped with the uniform convergence norm which, by abuse of language, is denoted as
$AP(\mathbb {R}, X)$
is a Banach space equipped with the uniform convergence norm which, by abuse of language, is denoted as
![]() $\|f\|:=\sup \{\|f(t)\|: t\in \mathbb {R}\}$
.
$\|f\|:=\sup \{\|f(t)\|: t\in \mathbb {R}\}$
.
On the one hand, as in the case of
![]() $AP(\mathbb {R},\mathbb {C})$
, Bohr’s definition of almost periodicity of a function
$AP(\mathbb {R},\mathbb {C})$
, Bohr’s definition of almost periodicity of a function
![]() $f\in AP(\mathbb {R},X)$
is also equivalent in this case to the property of relative compactness, called normality or Bochner-type property, for the family
$f\in AP(\mathbb {R},X)$
is also equivalent in this case to the property of relative compactness, called normality or Bochner-type property, for the family
![]() $\{f(t+h): h\in \mathbb {R}\}$
of translates of f [Reference Corduneanu10, Section 3.5].
$\{f(t+h): h\in \mathbb {R}\}$
of translates of f [Reference Corduneanu10, Section 3.5].
On the other hand, another very important result of this theory is the approximation theorem according to which the class of almost periodic functions
![]() $AP(\mathbb {R},X)$
coincides with the class of limit functions of uniformly convergent sequences of trigonometric polynomials of the type
$AP(\mathbb {R},X)$
coincides with the class of limit functions of uniformly convergent sequences of trigonometric polynomials of the type
with arbitrary real exponents
![]() $\lambda _j$
and arbitrary coefficients
$\lambda _j$
and arbitrary coefficients
![]() $a_j\in X$
[Reference Corduneanu10, Sections 3.5 and 4.5]. These approximating exponential polynomials can be found by Bochner–Fejér’s summation (see, in this regard, [Reference Besicovitch3, Chapter 1, Section 9], [Reference Corduneanu10, Section 4.5], or [Reference Amerio and Prouse1, Chapter 2, Section 3]). In fact, if a function
$a_j\in X$
[Reference Corduneanu10, Sections 3.5 and 4.5]. These approximating exponential polynomials can be found by Bochner–Fejér’s summation (see, in this regard, [Reference Besicovitch3, Chapter 1, Section 9], [Reference Corduneanu10, Section 4.5], or [Reference Amerio and Prouse1, Chapter 2, Section 3]). In fact, if a function
![]() $f(t)$
belongs to
$f(t)$
belongs to
![]() $AP(\mathbb {R},X)$
, then there exists a (Bochner–Fejér’s) sequence
$AP(\mathbb {R},X)$
, then there exists a (Bochner–Fejér’s) sequence
 $P_k^f(t)=\sum _{m=1}^nr_{m,k}a_me^{i\lambda _mt}$
of trigonometric polynomials of type (1.1) which satisfies the condition
$P_k^f(t)=\sum _{m=1}^nr_{m,k}a_me^{i\lambda _mt}$
of trigonometric polynomials of type (1.1) which satisfies the condition
 $\|f(t)-P_k^f(t)\|\to 0\ \mbox {as }k\to \infty $
, where the rational numbers
$\|f(t)-P_k^f(t)\|\to 0\ \mbox {as }k\to \infty $
, where the rational numbers
![]() $r_{m,k}$
depend on m and k, but not on
$r_{m,k}$
depend on m and k, but not on
![]() $a_m$
, and
$a_m$
, and
![]() $r_{m,k}\to 1$
as
$r_{m,k}\to 1$
as
![]() $k\to \infty $
.
$k\to \infty $
.
Moreover, for any function
![]() $f\in AP(\mathbb {R},X)$
, the mean value
$f\in AP(\mathbb {R},X)$
, the mean value
 $$ \begin{align*} M(f(t))=\lim_{l\to\infty}\frac{ 1}{ l}\int_{a}^{a+l}f(t)\,dt \end{align*} $$
$$ \begin{align*} M(f(t))=\lim_{l\to\infty}\frac{ 1}{ l}\int_{a}^{a+l}f(t)\,dt \end{align*} $$
exists uniformly with respect to
![]() $a\in \mathbb {R}$
, and, at most, a countable set of values of
$a\in \mathbb {R}$
, and, at most, a countable set of values of
![]() $\lambda _k\in \mathbb {R}$
such that
$\lambda _k\in \mathbb {R}$
such that
![]() $a_k=a(f,\lambda _k) = M(f(t)e^{-\lambda _k t})\in X$
is different from the null element in X [Reference Corduneanu10, Sections 3.5 and 4.5]. In this way, the series
$a_k=a(f,\lambda _k) = M(f(t)e^{-\lambda _k t})\in X$
is different from the null element in X [Reference Corduneanu10, Sections 3.5 and 4.5]. In this way, the series
![]() $\sum _{k\geq 1}a_ke^{i\lambda _kt}$
is called the Fourier series of f [Reference Corduneanu10, Section 4.5]. The elements
$\sum _{k\geq 1}a_ke^{i\lambda _kt}$
is called the Fourier series of f [Reference Corduneanu10, Section 4.5]. The elements
![]() $a_k$
and
$a_k$
and
![]() $\lambda _k$
are also called the Fourier coefficients and exponents of f, respectively. It is worth noting that if two functions
$\lambda _k$
are also called the Fourier coefficients and exponents of f, respectively. It is worth noting that if two functions
![]() $f_1(t)$
and
$f_1(t)$
and
![]() $f_2(t)$
in
$f_2(t)$
in
![]() $AP(\mathbb {R},X)$
have identical Fourier series, then they are equal (see [Reference Amerio and Prouse1, p. 25] or [Reference Corduneanu10, Section 4.5]).
$AP(\mathbb {R},X)$
have identical Fourier series, then they are equal (see [Reference Amerio and Prouse1, p. 25] or [Reference Corduneanu10, Section 4.5]).
In this paper, we consider an equivalence relation on the functions with values in a Banach space X which can be represented with a Fourier-like series (see the comments before Definition 3.2), and which satisfies the important property consisting of that an equivalence class is completely contained in the space
![]() $AP(\mathbb {R},X)$
when at least one of its functions is almost periodic (see Corollary 3.3). In this way, by analogy with the recent developments which we made for the space
$AP(\mathbb {R},X)$
when at least one of its functions is almost periodic (see Corollary 3.3). In this way, by analogy with the recent developments which we made for the space
![]() $AP(\mathbb {R},\mathbb {C})$
, the Besicovitch almost periodic functions, and other spaces of generalized almost periodic functions (see [Reference Sepulcre and Vidal16, Reference Sepulcre and Vidal17, Reference Sepulcre and Vidal19], respectively), this equivalence relation leads to refine the Bochner-type property or normality in the sense that the condition of almost periodicity in
$AP(\mathbb {R},\mathbb {C})$
, the Besicovitch almost periodic functions, and other spaces of generalized almost periodic functions (see [Reference Sepulcre and Vidal16, Reference Sepulcre and Vidal17, Reference Sepulcre and Vidal19], respectively), this equivalence relation leads to refine the Bochner-type property or normality in the sense that the condition of almost periodicity in
![]() $AP(\mathbb {R},X)$
implies that every sequence of translates has a subsequence that converges, with respect to the topology of
$AP(\mathbb {R},X)$
implies that every sequence of translates has a subsequence that converges, with respect to the topology of
![]() $AP(\mathbb {R},X)$
, to an equivalent function (see Theorem 3.7 and Corollary 3.8). This extends our previous work on the case of numerical almost periodic functions (see [Reference Sepulcre and Vidal16, Reference Sepulcre and Vidal17], but also [Reference Sepulcre and Vidal18, Reference Sepulcre and Vidal20]). Moreover, we point out that the proof given here of the main result, and specifically that of Lemma 3.2, is different from those of previous papers.
$AP(\mathbb {R},X)$
, to an equivalent function (see Theorem 3.7 and Corollary 3.8). This extends our previous work on the case of numerical almost periodic functions (see [Reference Sepulcre and Vidal16, Reference Sepulcre and Vidal17], but also [Reference Sepulcre and Vidal18, Reference Sepulcre and Vidal20]). Moreover, we point out that the proof given here of the main result, and specifically that of Lemma 3.2, is different from those of previous papers.
2 Preliminaries
Let
![]() $(X,\|\cdot \|)$
be an arbitrary Banach space over
$(X,\|\cdot \|)$
be an arbitrary Banach space over
![]() $\mathbb {C}$
. We shall refer to the expressions of the type
$\mathbb {C}$
. We shall refer to the expressions of the type
 $$ \begin{align*}a_1e^{i\lambda_1p}+\cdots+a_je^{i\lambda_jp}+\cdots\end{align*} $$
$$ \begin{align*}a_1e^{i\lambda_1p}+\cdots+a_je^{i\lambda_jp}+\cdots\end{align*} $$
as exponential sums, where the
![]() $\lambda _j$
’s are real numbers, the
$\lambda _j$
’s are real numbers, the
![]() $a_j$
’s are in X, and p is the variable. For our purposes, we next consider the following classes.
$a_j$
’s are in X, and p is the variable. For our purposes, we next consider the following classes.
Definition 2.1 Let
![]() $\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
be an arbitrary countable set of distinct real numbers, which we will call a set of exponents or frequencies. We will say that an exponential sum is in the class
$\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
be an arbitrary countable set of distinct real numbers, which we will call a set of exponents or frequencies. We will say that an exponential sum is in the class
![]() $\mathcal {S}_{\Lambda }^X$
if it is a formal series of type
$\mathcal {S}_{\Lambda }^X$
if it is a formal series of type
 $$ \begin{align*} \sum_{j\geq 1}a_je^{i\lambda_jp},\ a_j\in X,\ \lambda_j\in\Lambda. \end{align*} $$
$$ \begin{align*} \sum_{j\geq 1}a_je^{i\lambda_jp},\ a_j\in X,\ \lambda_j\in\Lambda. \end{align*} $$
In the next section of this paper, we are going to consider some functions which are associated with a concrete subclass of these exponential sums, where the parameter p will be changed by
![]() $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
By analogy with [Reference Sepulcre and Vidal17, Definition 2], we next consider the following equivalence relation on the classes
![]() $\mathcal {S}_{\Lambda }^X$
.
$\mathcal {S}_{\Lambda }^X$
.
Definition 2.2 Given an arbitrary countable set
![]() $\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
of distinct real numbers, consider
$\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
of distinct real numbers, consider
![]() $A_1(p)$
and
$A_1(p)$
and
![]() $A_2(p)$
two exponential sums in the class
$A_2(p)$
two exponential sums in the class
![]() $\mathcal {S}_{\Lambda }^X$
, say
$\mathcal {S}_{\Lambda }^X$
, say
 $A_1(p)=\sum _{j\geq 1}a_je^{i\lambda _jp}$
and
$A_1(p)=\sum _{j\geq 1}a_je^{i\lambda _jp}$
and
 $A_2(p)=\sum _{j\geq 1}b_je^{i\lambda _jp}.$
We will say that
$A_2(p)=\sum _{j\geq 1}b_je^{i\lambda _jp}.$
We will say that
![]() $A_1$
is
$A_1$
is
![]() $^*$
-equivalent to
$^*$
-equivalent to
![]() $A_2$
(in that case, we will write
$A_2$
(in that case, we will write
![]() ) if for each integer value
) if for each integer value
![]() $n\geq 1$
, with
$n\geq 1$
, with
![]() $n\leq \sharp \Lambda $
, there exists a
$n\leq \sharp \Lambda $
, there exists a
![]() $\mathbb {Q}$
-linear map
$\mathbb {Q}$
-linear map
![]() $\psi _n:V_n\to \mathbb {R}$
, where
$\psi _n:V_n\to \mathbb {R}$
, where
![]() $V_n$
is the
$V_n$
is the
![]() $\mathbb {Q}$
-vector space generated by
$\mathbb {Q}$
-vector space generated by
![]() $\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
, such that
$\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
, such that
 $$ \begin{align*}b_j=a_je^{i\psi_n(\lambda_j)},\ j=1,\ldots,n.\end{align*} $$
$$ \begin{align*}b_j=a_je^{i\psi_n(\lambda_j)},\ j=1,\ldots,n.\end{align*} $$
As we next show, this equivalence relation can be characterized in terms of a basis for the set of exponents
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $G_{\Lambda }=\{g_1, g_2,\ldots , g_k,\ldots \}$
be a basis of the vector space over the rationals generated by a set
$G_{\Lambda }=\{g_1, g_2,\ldots , g_k,\ldots \}$
be a basis of the vector space over the rationals generated by a set
![]() $\Lambda $
of exponents, which yields that
$\Lambda $
of exponents, which yields that
![]() $G_{\Lambda }$
is linearly independent over the rational numbers and each
$G_{\Lambda }$
is linearly independent over the rational numbers and each
![]() $\lambda _j$
is expressible as a finite linear combination of terms of
$\lambda _j$
is expressible as a finite linear combination of terms of
![]() $G_{\Lambda }$
, say
$G_{\Lambda }$
, say
 $$ \begin{align} \lambda_j=\sum_{k=1}^{q_j}r_{j,k}g_k,\ \mbox{for some }r_{j,k}\in\mathbb{Q}. \end{align} $$
$$ \begin{align} \lambda_j=\sum_{k=1}^{q_j}r_{j,k}g_k,\ \mbox{for some }r_{j,k}\in\mathbb{Q}. \end{align} $$
By abuse of notation, we will say that
![]() $G_{\Lambda }$
is a basis for
$G_{\Lambda }$
is a basis for
![]() $\Lambda $
. Moreover, we will say that
$\Lambda $
. Moreover, we will say that
![]() $G_{\Lambda }$
is an integral basis for
$G_{\Lambda }$
is an integral basis for
![]() $\Lambda $
when
$\Lambda $
when
![]() $r_{j,k}\in \mathbb {Z}$
for any
$r_{j,k}\in \mathbb {Z}$
for any
![]() $j,k$
. For completeness, we will provide the proof of the following result that allows us to characterize the equivalence relation introduced in Definition 2.2.
$j,k$
. For completeness, we will provide the proof of the following result that allows us to characterize the equivalence relation introduced in Definition 2.2.
Proposition 2.1 Given
![]() $\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
a set of exponents, consider
$\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
a set of exponents, consider
![]() $A_1(p)$
and
$A_1(p)$
and
![]() $A_2(p)$
two exponential sums in the class
$A_2(p)$
two exponential sums in the class
![]() $\mathcal {S}_{\Lambda }^X$
, say
$\mathcal {S}_{\Lambda }^X$
, say
 $A_1(p)=\sum _{j\geq 1}a_je^{i\lambda _jp}$
and
$A_1(p)=\sum _{j\geq 1}a_je^{i\lambda _jp}$
and
 $A_2(p)=\sum _{j\geq 1}b_je^{i\lambda _jp}.$
Fixed a basis
$A_2(p)=\sum _{j\geq 1}b_je^{i\lambda _jp}.$
Fixed a basis
![]() $G_{\Lambda }$
for
$G_{\Lambda }$
for
![]() $\Lambda $
, for each
$\Lambda $
, for each
![]() $j\geq 1$
, let
$j\geq 1$
, let
![]() $\mathbf {r}_j$
be the vector of rational components satisfying (2.1). Then
$\mathbf {r}_j$
be the vector of rational components satisfying (2.1). Then
![]() if and only if for each integer value
if and only if for each integer value
![]() $n\geq 1$
, with
$n\geq 1$
, with
![]() $n\leq \sharp \Lambda $
, there exists a vector
$n\leq \sharp \Lambda $
, there exists a vector
![]() $\mathbf {x}_n=(x_{n,1},x_{n,2},\ldots ,x_{n,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
$\mathbf {x}_n=(x_{n,1},x_{n,2},\ldots ,x_{n,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
![]() $b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_n>i}$
for
$b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_n>i}$
for
![]() $j=1,2,\ldots ,n$
. Furthermore, if
$j=1,2,\ldots ,n$
. Furthermore, if
![]() $G_{\Lambda }$
is an integral basis for
$G_{\Lambda }$
is an integral basis for
![]() $\Lambda $
, then
$\Lambda $
, then
![]() if and only if there exists
if and only if there exists
![]() $\mathbf {x}_0=(x_{0,1},x_{0,2},\ldots ,x_{0,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
$\mathbf {x}_0=(x_{0,1},x_{0,2},\ldots ,x_{0,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
![]() $b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_0>i}$
for every
$b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_0>i}$
for every
![]() $j\geq 1$
.
$j\geq 1$
.
Proof For each integer value
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $V_n$
be the
$V_n$
be the
![]() $\mathbb {Q}$
-vector space generated by
$\mathbb {Q}$
-vector space generated by
![]() $\{\lambda _1,\ldots ,\lambda _n\}$
, V the
$\{\lambda _1,\ldots ,\lambda _n\}$
, V the
![]() $\mathbb {Q}$
-vector space generated by
$\mathbb {Q}$
-vector space generated by
![]() $\Lambda $
, and
$\Lambda $
, and
![]() $G_{\Lambda }=\{g_1, g_2,\ldots , g_k,\ldots \}$
a basis of V. If
$G_{\Lambda }=\{g_1, g_2,\ldots , g_k,\ldots \}$
a basis of V. If
![]() and n is a positive integer number with
and n is a positive integer number with
![]() $n\leq \sharp \Lambda $
, by Definition 2.2, there exists a
$n\leq \sharp \Lambda $
, by Definition 2.2, there exists a
![]() $\mathbb {Q}$
-linear map
$\mathbb {Q}$
-linear map
![]() $\psi _n:V_n\to \mathbb {R}$
such that
$\psi _n:V_n\to \mathbb {R}$
such that
 $b_j=a_je^{i\psi _n(\lambda _j)},\ j=1,2\ldots ,n.$
Hence,
$b_j=a_je^{i\psi _n(\lambda _j)},\ j=1,2\ldots ,n.$
Hence,
 $b_j=a_je^{i\sum _{k=1}^{i_j}r_{j,k}\psi _n(g_k)},\ j=1,2,\ldots ,n$
, or, equivalently,
$b_j=a_je^{i\sum _{k=1}^{i_j}r_{j,k}\psi _n(g_k)},\ j=1,2,\ldots ,n$
, or, equivalently,
![]() $b_j=a_j e^{i<\mathbf {r}_j,\mathbf {x}_n>},\ j=1,2,\ldots ,n,$
with
$b_j=a_j e^{i<\mathbf {r}_j,\mathbf {x}_n>},\ j=1,2,\ldots ,n,$
with
![]() $\mathbf {x}_n:=(\psi _n(g_1),\psi _n(g_2),\ldots ,\psi _n(g_p),0,\ldots )$
, where
$\mathbf {x}_n:=(\psi _n(g_1),\psi _n(g_2),\ldots ,\psi _n(g_p),0,\ldots )$
, where
![]() $p=\max \{i_1,i_2,\ldots ,i_n\}$
. Conversely, suppose the existence, for each integer value
$p=\max \{i_1,i_2,\ldots ,i_n\}$
. Conversely, suppose the existence, for each integer value
![]() $n\geq 1$
, of a vector
$n\geq 1$
, of a vector
![]() $\mathbf {x}_n=(x_{n,1},x_{n,2},\ldots ,x_{n,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
$\mathbf {x}_n=(x_{n,1},x_{n,2},\ldots ,x_{n,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
![]() $b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_n>i}$
,
$b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_n>i}$
,
![]() $j=1,2,\ldots ,n$
. Thus, a
$j=1,2,\ldots ,n$
. Thus, a
![]() $\mathbb {Q}$
-linear map
$\mathbb {Q}$
-linear map
![]() $\psi _n:V_n\to \mathbb {R}$
can be defined from
$\psi _n:V_n\to \mathbb {R}$
can be defined from
![]() $\psi _n(g_k):=x_{n,k}$
,
$\psi _n(g_k):=x_{n,k}$
,
![]() $k\geq 1$
. Therefore,
$k\geq 1$
. Therefore,
 $\psi _n(\lambda _j)=\sum _{k=1}^{i_j}r_{j,k}\psi (g_k)= <\mathbf {r}_j,\mathbf {x}_n>,\ j=1,2,\ldots ,n,$
and the result follows.
$\psi _n(\lambda _j)=\sum _{k=1}^{i_j}r_{j,k}\psi (g_k)= <\mathbf {r}_j,\mathbf {x}_n>,\ j=1,2,\ldots ,n,$
and the result follows.
Now, suppose that
![]() $G_{\Lambda }$
is an integral basis for
$G_{\Lambda }$
is an integral basis for
![]() $\Lambda $
and
$\Lambda $
and
![]() . By above, for each given integer value
. By above, for each given integer value
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\mathbf {x}_n=(x_{n,1},x_{n,2},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
be a vector such that
$\mathbf {x}_n=(x_{n,1},x_{n,2},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
be a vector such that
![]() $b_j=a_j e^{i<\mathbf {r}_j,\mathbf {x}_n>},\ j=1,2,\ldots ,n.$
Since each component of
$b_j=a_j e^{i<\mathbf {r}_j,\mathbf {x}_n>},\ j=1,2,\ldots ,n.$
Since each component of
![]() $\mathbf {r}_j$
is an integer number, without loss of generality, we can take
$\mathbf {r}_j$
is an integer number, without loss of generality, we can take
![]() $\mathbf {x}_n\in [0,2\pi )^{\sharp G_{\Lambda }}$
as the unique vector in
$\mathbf {x}_n\in [0,2\pi )^{\sharp G_{\Lambda }}$
as the unique vector in
![]() $[0,2\pi )^{\sharp G_{\Lambda }}$
satisfying the above equalities, where we assume
$[0,2\pi )^{\sharp G_{\Lambda }}$
satisfying the above equalities, where we assume
![]() $x_{n,k}=0$
for any k such that
$x_{n,k}=0$
for any k such that
![]() $r_{j,k}=0$
, for
$r_{j,k}=0$
, for
![]() $j=1,\ldots ,n$
. Therefore, under this assumption, if
$j=1,\ldots ,n$
. Therefore, under this assumption, if
![]() $m>n$
, then
$m>n$
, then
![]() $x_{m,k}=x_{n,k}$
for any k, so that
$x_{m,k}=x_{n,k}$
for any k, so that
![]() $x_{n,k}\neq 0$
. In this way, we can construct a vector
$x_{n,k}\neq 0$
. In this way, we can construct a vector
![]() $\mathbf {x}_0=(x_{0,1},x_{0,2},\ldots ,x_{0,k},\ldots )\in [0,2\pi )^{\sharp G_{\Lambda }}$
such that
$\mathbf {x}_0=(x_{0,1},x_{0,2},\ldots ,x_{0,k},\ldots )\in [0,2\pi )^{\sharp G_{\Lambda }}$
such that
![]() $b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_0>i}$
, for every
$b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_0>i}$
, for every
![]() $j\geq 1$
. Indeed, if
$j\geq 1$
. Indeed, if
![]() $r_{1,k}\neq 0$
, then the component
$r_{1,k}\neq 0$
, then the component
![]() $x_{0,k}$
is chosen as
$x_{0,k}$
is chosen as
![]() $x_{1,k}$
, and if
$x_{1,k}$
, and if
![]() $r_{1,k}=0$
, then each component
$r_{1,k}=0$
, then each component
![]() $x_{0,k}$
is defined as
$x_{0,k}$
is defined as
![]() $x_{n+1,k}$
, where
$x_{n+1,k}$
, where
![]() $r_{j,k}=0$
, for
$r_{j,k}=0$
, for
![]() $j=1,\ldots ,n$
, and
$j=1,\ldots ,n$
, and
![]() $r_{n+1,k}\neq 0$
. Conversely, if there exists
$r_{n+1,k}\neq 0$
. Conversely, if there exists
![]() $\mathbf {x}_0=(x_{0,1},x_{0,2},\ldots ,x_{0,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
$\mathbf {x}_0=(x_{0,1},x_{0,2},\ldots ,x_{0,k},\ldots )\in \mathbb {R}^{\sharp G_{\Lambda }}$
such that
![]() $b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_0>i}$
, for every
$b_j=a_j e^{<\mathbf {r}_j,\mathbf {x}_0>i}$
, for every
![]() $j\geq 1$
, then it is clear that
$j\geq 1$
, then it is clear that
![]() under Definition 2.2. ▪
under Definition 2.2. ▪
3 Main results
Depending on the set of Fourier exponents, we next consider the following classes of almost periodic functions in
![]() $AP(\mathbb {R},X)$
.
$AP(\mathbb {R},X)$
.
Definition 3.1 Let
![]() $\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
be an arbitrary countable set of distinct real numbers. We will say that a function
$\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
be an arbitrary countable set of distinct real numbers. We will say that a function
![]() $f:\mathbb {R}\to X$
is in the class
$f:\mathbb {R}\to X$
is in the class
![]() $\mathcal {F}_{\Lambda }^X$
if it is an almost periodic function in
$\mathcal {F}_{\Lambda }^X$
if it is an almost periodic function in
![]() $AP(\mathbb {R},X)$
whose associated Fourier series is of the form
$AP(\mathbb {R},X)$
whose associated Fourier series is of the form
 $$ \begin{align} \sum_{j\geq 1}a_je^{i\lambda_jt},\ a_j\in X,\ \lambda_j\in\Lambda. \end{align} $$
$$ \begin{align} \sum_{j\geq 1}a_je^{i\lambda_jt},\ a_j\in X,\ \lambda_j\in\Lambda. \end{align} $$
In the particular case that
![]() $\Lambda =\{\lambda _1,\ldots ,\lambda _n\}$
is finite, the functions in
$\Lambda =\{\lambda _1,\ldots ,\lambda _n\}$
is finite, the functions in
![]() $\mathcal {F}_{\Lambda }^X$
are finite exponential sums of the form
$\mathcal {F}_{\Lambda }^X$
are finite exponential sums of the form
 $$ \begin{align*} a_1e^{i\lambda_1t}+\cdots+a_ne^{i\lambda_nt},\ a_j\in X,\ \lambda_j\in\Lambda,\ j=1,\ldots,n. \end{align*} $$
$$ \begin{align*} a_1e^{i\lambda_1t}+\cdots+a_ne^{i\lambda_nt},\ a_j\in X,\ \lambda_j\in\Lambda,\ j=1,\ldots,n. \end{align*} $$
In terms of Definition 2.2, we next define an equivalence relation on a certain space of functions with values in a Banach space X which can be represented by exponential sums of the form (3.1), and in particular on the classes
![]() $\mathcal {F}_{\Lambda }^X$
. More specifically, the next equivalence relation is defined on the set, say
$\mathcal {F}_{\Lambda }^X$
. More specifically, the next equivalence relation is defined on the set, say
![]() $\mathcal {A}(\mathbb {R},X)$
, of functions f from
$\mathcal {A}(\mathbb {R},X)$
, of functions f from
![]() $\mathbb {R}$
to X for which there exists the mean value
$\mathbb {R}$
to X for which there exists the mean value
 $$ \begin{align*}M\{f(t)\}:=\lim_{l\to\infty}\frac{1 }{ 2l}\int_{-l}^l f(t)dt\in X,\end{align*} $$
$$ \begin{align*}M\{f(t)\}:=\lim_{l\to\infty}\frac{1 }{ 2l}\int_{-l}^l f(t)dt\in X,\end{align*} $$
![]() $f(t)e^{-i\lambda t}\in \mathcal {A}(\mathbb {R},X)$
for any
$f(t)e^{-i\lambda t}\in \mathcal {A}(\mathbb {R},X)$
for any
![]() $\lambda \in \mathbb {R}$
, and there always exists at most a countable infinite set of real values
$\lambda \in \mathbb {R}$
, and there always exists at most a countable infinite set of real values
![]() $\lambda _k$
for which
$\lambda _k$
for which
![]() $a(f,\lambda _k):=M\{f(t)e^{-it\lambda _k}\}\neq 0.$
In this way, we can associate to
$a(f,\lambda _k):=M\{f(t)e^{-it\lambda _k}\}\neq 0.$
In this way, we can associate to
![]() $f\in \mathcal {A}(\mathbb {R},X)$
a unique exponential sum
$f\in \mathcal {A}(\mathbb {R},X)$
a unique exponential sum
 $\sum _{\lambda _k\in \Lambda }a(f,\lambda _k)e^{i\lambda _k t}$
, where
$\sum _{\lambda _k\in \Lambda }a(f,\lambda _k)e^{i\lambda _k t}$
, where
![]() $\Lambda =\{\lambda _k\in \mathbb {R}:a(f,\lambda _k)\neq 0\}$
, which is of the form (3.1) and which we will call its Fourier series. It is clear that
$\Lambda =\{\lambda _k\in \mathbb {R}:a(f,\lambda _k)\neq 0\}$
, which is of the form (3.1) and which we will call its Fourier series. It is clear that
![]() $AP(\mathbb {R},X)\subset \mathcal {A}(\mathbb {R},X)$
, where X stands for a Banach space, satisfies this property (diverse types of almost periodic functions with values in Banach spaces which can be represented by its Fourier-like series can be seen in [Reference Chérif9]). Furthermore, if
$AP(\mathbb {R},X)\subset \mathcal {A}(\mathbb {R},X)$
, where X stands for a Banach space, satisfies this property (diverse types of almost periodic functions with values in Banach spaces which can be represented by its Fourier-like series can be seen in [Reference Chérif9]). Furthermore, if
![]() $X=\mathbb {C}$
, every function in the Besicovitch space
$X=\mathbb {C}$
, every function in the Besicovitch space
![]() $B(\mathbb {R},\mathbb {C})\supset AP(\mathbb {R},\mathbb {C})$
satisfies this property (see [Reference Corduneanu10, Section 3.4]).
$B(\mathbb {R},\mathbb {C})\supset AP(\mathbb {R},\mathbb {C})$
satisfies this property (see [Reference Corduneanu10, Section 3.4]).
Definition 3.2 Given
![]() $\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
a set of exponents, let
$\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _j,\ldots \}$
a set of exponents, let
![]() $f_1$
and
$f_1$
and
![]() $f_2$
denote two functions in
$f_2$
denote two functions in
![]() $\mathcal {A}(\mathbb {R},X)$
which are, respectively, associated with exponential sums of the form
$\mathcal {A}(\mathbb {R},X)$
which are, respectively, associated with exponential sums of the form
 $$ \begin{align*} \sum_{j\geq 1}a_je^{i\lambda_jt}\ \mbox{and}\ \sum_{j\geq 1}b_je^{i\lambda_jt},\ a_j,b_j\in X,\ \lambda_j\in\Lambda. \end{align*} $$
$$ \begin{align*} \sum_{j\geq 1}a_je^{i\lambda_jt}\ \mbox{and}\ \sum_{j\geq 1}b_je^{i\lambda_jt},\ a_j,b_j\in X,\ \lambda_j\in\Lambda. \end{align*} $$
We will say that
![]() $f_1$
is
$f_1$
is
![]() $^*$
-equivalent to
$^*$
-equivalent to
![]() $f_2$
if for each integer value
$f_2$
if for each integer value
![]() $n\geq 1$
, with
$n\geq 1$
, with
![]() $n\leq \sharp \Lambda $
, there exists a
$n\leq \sharp \Lambda $
, there exists a
![]() $\mathbb {Q}$
-linear map
$\mathbb {Q}$
-linear map
![]() $\psi _n:V_n\to \mathbb {R}$
, where
$\psi _n:V_n\to \mathbb {R}$
, where
![]() $V_n$
is the
$V_n$
is the
![]() $\mathbb {Q}$
-vector space generated by
$\mathbb {Q}$
-vector space generated by
![]() $\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
, such that
$\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
, such that
 $$ \begin{align*}b_j=a_je^{i\psi_n(\lambda_j)},\ j=1,\ldots,n.\end{align*} $$
$$ \begin{align*}b_j=a_je^{i\psi_n(\lambda_j)},\ j=1,\ldots,n.\end{align*} $$
In that case, we will write
 .
.
Recall that if two functions
![]() $f_1(t)$
and
$f_1(t)$
and
![]() $f_2(t)$
in
$f_2(t)$
in
![]() $AP(\mathbb {R},X)$
have identical Fourier series, then they are equal. As we can see, restricted to actual series of almost periodic functions, the
$AP(\mathbb {R},X)$
have identical Fourier series, then they are equal. As we can see, restricted to actual series of almost periodic functions, the
![]() $^*$
-equivalence of formal series (Definition 2.2) reduces to that on the functions in the classes
$^*$
-equivalence of formal series (Definition 2.2) reduces to that on the functions in the classes
![]() $\mathcal {F}_{\Lambda }^X$
. That is why we use the same notation for them.
$\mathcal {F}_{\Lambda }^X$
. That is why we use the same notation for them.
In the context of finite exponential sums (when
![]() $\Lambda $
is finite), the following proposition is useful to get the subsequent results in this paper. By analogy with the case of
$\Lambda $
is finite), the following proposition is useful to get the subsequent results in this paper. By analogy with the case of
![]() $AP(\mathbb {R},\mathbb {C})$
with the topology of the uniform convergence, its proof is based on the fact that the functions in
$AP(\mathbb {R},\mathbb {C})$
with the topology of the uniform convergence, its proof is based on the fact that the functions in
![]() $\mathcal {F}_{\Lambda }^X$
are also equipped with the uniform convergence norm. Hence, the proof of the next result is analogous to that of [Reference Sepulcre and Vidal16, Theorem 1].
$\mathcal {F}_{\Lambda }^X$
are also equipped with the uniform convergence norm. Hence, the proof of the next result is analogous to that of [Reference Sepulcre and Vidal16, Theorem 1].
Proposition 3.1 Given
![]() $\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
a finite set of exponents, let
$\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
a finite set of exponents, let
 $f_1(t)=\sum _{j=1}^na_je^{i\lambda _j t}$
and
$f_1(t)=\sum _{j=1}^na_je^{i\lambda _j t}$
and
 $f_2(t)=\sum _{j=1}^nb_je^{i\lambda _j t}$
be two
$f_2(t)=\sum _{j=1}^nb_je^{i\lambda _j t}$
be two
![]() $^*$
-equivalent functions in the class
$^*$
-equivalent functions in the class
![]() $\mathcal {F}_{\Lambda }^X$
. Fixed
$\mathcal {F}_{\Lambda }^X$
. Fixed
![]() $\varepsilon>0$
, there exists a relatively dense set of real numbers
$\varepsilon>0$
, there exists a relatively dense set of real numbers
![]() $\{\tau \}$
such that
$\{\tau \}$
such that
We next prove the following result which is essential in our subsequent development. Given an arbitrary set
![]() $\Lambda $
of exponents and two exponential sums
$\Lambda $
of exponents and two exponential sums
![]() $A_1(t),A_2(t)\in \mathcal {S}_{\Lambda }^X$
, suppose that
$A_1(t),A_2(t)\in \mathcal {S}_{\Lambda }^X$
, suppose that
![]() $A_1(t)$
is associated with an almost periodic function in
$A_1(t)$
is associated with an almost periodic function in
![]() $AP(\mathbb {R},X)$
and
$AP(\mathbb {R},X)$
and
 (under Definition 2.2), then is the exponential sum
(under Definition 2.2), then is the exponential sum
![]() $A_2(t)$
associated with an almost periodic function in
$A_2(t)$
associated with an almost periodic function in
![]() $AP(\mathbb {R},X)$
? The next lemma answers affirmatively this question.
$AP(\mathbb {R},X)$
? The next lemma answers affirmatively this question.
Lemma 3.2 Let
![]() $f_1(t)\in AP(\mathbb {R},X)$
be an almost periodic function whose Fourier series is given by
$f_1(t)\in AP(\mathbb {R},X)$
be an almost periodic function whose Fourier series is given by
 $\sum _{j\geq 1}a_je^{i\lambda _jt}, a_j\in X$
, where
$\sum _{j\geq 1}a_je^{i\lambda _jt}, a_j\in X$
, where
![]() $\{\lambda _1,\ldots ,\lambda _j,\ldots \}$
is a set of distinct exponents. Consider
$\{\lambda _1,\ldots ,\lambda _j,\ldots \}$
is a set of distinct exponents. Consider
![]() $b_j\in X$
such that
$b_j\in X$
such that
 $\sum _{j\geq 1}b_je^{i\lambda _jt}$
and
$\sum _{j\geq 1}b_je^{i\lambda _jt}$
and
 $\sum _{j\geq 1}a_je^{i\lambda _jt}$
are
$\sum _{j\geq 1}a_je^{i\lambda _jt}$
are
![]() $^*$
-equivalent. Then
$^*$
-equivalent. Then
 $\sum _{j\geq 1}b_je^{i\lambda _jt}$
is the Fourier series associated with an almost periodic function
$\sum _{j\geq 1}b_je^{i\lambda _jt}$
is the Fourier series associated with an almost periodic function
![]() $f_2(t)\in AP(\mathbb {R},X)$
satisfying
$f_2(t)\in AP(\mathbb {R},X)$
satisfying
 .
.
Proof Take
![]() $\Lambda =\{\lambda _1,\ldots ,\lambda _j,\ldots \}$
. By hypothesis,
$\Lambda =\{\lambda _1,\ldots ,\lambda _j,\ldots \}$
. By hypothesis,
![]() $f_1\in \mathcal {F}_{\Lambda }^X\subset AP(\mathbb {R},X)$
is determined by a series of the form
$f_1\in \mathcal {F}_{\Lambda }^X\subset AP(\mathbb {R},X)$
is determined by a series of the form
 $\sum _{j\geq 1}a_je^{i\lambda _jt},\ a_j\in X,\ \lambda _j\in \Lambda .$
In virtue from [Reference Amerio and Prouse1, p. 29] or [Reference Corduneanu10, Section 4.5], let
$\sum _{j\geq 1}a_je^{i\lambda _jt},\ a_j\in X,\ \lambda _j\in \Lambda .$
In virtue from [Reference Amerio and Prouse1, p. 29] or [Reference Corduneanu10, Section 4.5], let
 $P_{k}^{f_1}(t)=\sum _{j\geq 1}p_{j,k}a_{j}e^{i\lambda _jt}$
,
$P_{k}^{f_1}(t)=\sum _{j\geq 1}p_{j,k}a_{j}e^{i\lambda _jt}$
,
![]() $k=1,2,\ldots $
, be the Bochner–Fejér trigonometric polynomials which converge to
$k=1,2,\ldots $
, be the Bochner–Fejér trigonometric polynomials which converge to
![]() $f_1$
with respect to the topology of
$f_1$
with respect to the topology of
![]() $AP(\mathbb {R},X)$
(and converge formally to its Fourier series on
$AP(\mathbb {R},X)$
(and converge formally to its Fourier series on
![]() $\mathbb {R}$
). Now, take
$\mathbb {R}$
). Now, take
![]() $\tau \in \mathbb {R}$
, then
$\tau \in \mathbb {R}$
, then
 $P_{k}^{f_{1,\tau }}(t)=\sum _{j\geq 1}p_{j,k}a_{j}e^{i\lambda _j(t+\tau )}$
,
$P_{k}^{f_{1,\tau }}(t)=\sum _{j\geq 1}p_{j,k}a_{j}e^{i\lambda _j(t+\tau )}$
,
![]() $k=1,2,\ldots $
, are the Bochner–Fejér trigonometric polynomials which converge to
$k=1,2,\ldots $
, are the Bochner–Fejér trigonometric polynomials which converge to
![]() $f_{1,\tau }(t):=f_1(t+\tau )$
,
$f_{1,\tau }(t):=f_1(t+\tau )$
,
![]() $t\in \mathbb {R}$
. On the other hand, consider the finite exponential sums
$t\in \mathbb {R}$
. On the other hand, consider the finite exponential sums
 $\sum _{j\geq 1}p_{j,k}b_{j}e^{i\lambda _jt}$
, with
$\sum _{j\geq 1}p_{j,k}b_{j}e^{i\lambda _jt}$
, with
![]() $t\in \mathbb {R}$
and
$t\in \mathbb {R}$
and
![]() $k=1,2,\ldots $
. Take a positive sequence
$k=1,2,\ldots $
. Take a positive sequence
![]() $\{\varepsilon _l\}_{l\geq 1}$
tending to
$\{\varepsilon _l\}_{l\geq 1}$
tending to
![]() $0$
. By Proposition 3.1, given
$0$
. By Proposition 3.1, given
![]() $l\in \{1,2,\ldots \}$
, there exists a relatively dense set of real numbers
$l\in \{1,2,\ldots \}$
, there exists a relatively dense set of real numbers
![]() $\tau _l$
such that
$\tau _l$
such that
 $$ \begin{align*}\left\|\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_l)}-\sum_{j\geq 1}p_{j,k}b_{j}e^{i\lambda_jt}\right\|<\frac{\varepsilon_l}{3}\ \ \forall t\in\mathbb{R}\ \forall \tau_l.\end{align*} $$
$$ \begin{align*}\left\|\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_l)}-\sum_{j\geq 1}p_{j,k}b_{j}e^{i\lambda_jt}\right\|<\frac{\varepsilon_l}{3}\ \ \forall t\in\mathbb{R}\ \forall \tau_l.\end{align*} $$
Furthermore, by the Bochner–Féjer property, for each
![]() $l=1,2,\ldots $
, there exists
$l=1,2,\ldots $
, there exists
![]() $k_l\in \mathbb {N}$
such that
$k_l\in \mathbb {N}$
such that
 $$ \begin{align*}\left\|P_{k}^{f_{1,\tau_l}}(t)-f_1(t+\tau_l)\right\|=\left\|\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_l)}-f_1(t+\tau_l)\right\|\leq\frac{ \varepsilon_l}{ 3},\ \mbox{ for each }k>k_l.\end{align*} $$
$$ \begin{align*}\left\|P_{k}^{f_{1,\tau_l}}(t)-f_1(t+\tau_l)\right\|=\left\|\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_l)}-f_1(t+\tau_l)\right\|\leq\frac{ \varepsilon_l}{ 3},\ \mbox{ for each }k>k_l.\end{align*} $$
Finally, by the property of normality applied to the sequence
![]() $\{f_1(t+\tau _l)\}_{\tau _l}$
, we can extract a subsequence
$\{f_1(t+\tau _l)\}_{\tau _l}$
, we can extract a subsequence
![]() $\{f_1(t+\tau _{l_m})\}_{\tau _{l_m}}$
which converges to a certain function
$\{f_1(t+\tau _{l_m})\}_{\tau _{l_m}}$
which converges to a certain function
![]() $f_2$
with respect to the topology of
$f_2$
with respect to the topology of
![]() $AP(\mathbb {R},X)$
. In this way, we assure the existence of
$AP(\mathbb {R},X)$
. In this way, we assure the existence of
![]() $m_l\in \mathbb {N}$
such that
$m_l\in \mathbb {N}$
such that
 $$ \begin{align*}\left\|f_2(t)-f_1(t+\tau_{l_m})\right\|\leq\frac{\varepsilon}{3},\ \mbox{ for each }m>m_l.\end{align*} $$
$$ \begin{align*}\left\|f_2(t)-f_1(t+\tau_{l_m})\right\|\leq\frac{\varepsilon}{3},\ \mbox{ for each }m>m_l.\end{align*} $$
Now, given
![]() $l\geq 1$
, let
$l\geq 1$
, let
![]() $k>k_l$
and
$k>k_l$
and
![]() $m>m_l$
. We deduce from above that
$m>m_l$
. We deduce from above that
 $$ \begin{align*} &\left\|\sum_{j\geq 1}p_{j,k}b_{j}e^{i\lambda_jt}-f_2(t)\right\|\leq \left\|\sum_{j\geq 1}p_{j,k}b_{j}e^{i\lambda_jt}-\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_{l_m})}\right\|\\ &\qquad\qquad+\left\|\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_{l_m})}-f_1(t+\tau_{l_m})\right\|+ \left\|f_1(t+\tau_{l_m})-f_2(t)\right\| \leq \varepsilon_l. \end{align*} $$
$$ \begin{align*} &\left\|\sum_{j\geq 1}p_{j,k}b_{j}e^{i\lambda_jt}-f_2(t)\right\|\leq \left\|\sum_{j\geq 1}p_{j,k}b_{j}e^{i\lambda_jt}-\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_{l_m})}\right\|\\ &\qquad\qquad+\left\|\sum_{j\geq 1}p_{j,k}a_{j}e^{i\lambda_j(t+\tau_{l_m})}-f_1(t+\tau_{l_m})\right\|+ \left\|f_1(t+\tau_{l_m})-f_2(t)\right\| \leq \varepsilon_l. \end{align*} $$
Making l tend to infinity, we deduce that
 $\sum _{j\geq 1}p_{j,k}b_{j}e^{i\lambda _jt}$
,
$\sum _{j\geq 1}p_{j,k}b_{j}e^{i\lambda _jt}$
,
![]() $k=1,2,\ldots $
, converges to
$k=1,2,\ldots $
, converges to
![]() $f_2$
with respect to the topology of
$f_2$
with respect to the topology of
![]() $AP(\mathbb {R},X)$
. Likewise, since
$AP(\mathbb {R},X)$
. Likewise, since
![]() $AP(\mathbb {R},X)$
is the closure of the trigonometric polynomials with respect to the uniform convergence norm, we get that
$AP(\mathbb {R},X)$
is the closure of the trigonometric polynomials with respect to the uniform convergence norm, we get that
![]() $f_2\in AP(\mathbb {R},X)$
. Finally, by Definition 3.2, it is clear that
$f_2\in AP(\mathbb {R},X)$
. Finally, by Definition 3.2, it is clear that
 .▪
.▪
The reader can note that the proof of the previous result given here is different from those of [Reference Sepulcre and Vidal16, Lemma 2] and [Reference Sepulcre and Vidal17, Lemma 1].
As an immediate consequence of Lemma 3.2, the following result justifies the fact that an equivalence class (under Definition 3.2) is completely contained in
 when one of its functions is in
when one of its functions is in
![]() $\mathcal {F}_{\Lambda }^X$
.
$\mathcal {F}_{\Lambda }^X$
.
Corollary 3.3 Let
![]() $\Lambda $
be a set of exponents and
$\Lambda $
be a set of exponents and
![]() $\mathcal {G}$
an equivalence class of functions in
$\mathcal {G}$
an equivalence class of functions in
![]() $\mathcal {A}(\mathbb {R},X)$
(under Definition 3.2). If
$\mathcal {A}(\mathbb {R},X)$
(under Definition 3.2). If
![]() $f\in \mathcal {G}\cap \mathcal {F}_{\Lambda }^X$
, then
$f\in \mathcal {G}\cap \mathcal {F}_{\Lambda }^X$
, then
 .
.
As it can be seen below, the statements of many of the subsequent results include the condition that
![]() $\mathcal {G}$
is an equivalence class in
$\mathcal {G}$
is an equivalence class in
 . It is worth noting that Corollary 3.3 assures that this condition is satisfied when one of the functions in
. It is worth noting that Corollary 3.3 assures that this condition is satisfied when one of the functions in
![]() $\mathcal {G}$
belongs to
$\mathcal {G}$
belongs to
![]() $AP(\mathbb {R},X)$
.
$AP(\mathbb {R},X)$
.
We next prove that if
![]() $f_1(t)$
and
$f_1(t)$
and
![]() $f_2(t)$
are two
$f_2(t)$
are two
![]() $^*$
-equivalent almost periodic functions in some
$^*$
-equivalent almost periodic functions in some
![]() $\mathcal {F}_{\Lambda }^X$
, then
$\mathcal {F}_{\Lambda }^X$
, then
![]() $f_2(t)$
can be approximated by translates
$f_2(t)$
can be approximated by translates
![]() $\{f_1(t+\tau ):\tau \in \mathbb {R}\}$
of
$\{f_1(t+\tau ):\tau \in \mathbb {R}\}$
of
![]() $f_1(t)$
. This generalizes Proposition 3.1 for the case of a (nonnecessarily finite) arbitrary set of exponents. The main ingredient in order to prove this result for the case of functions with an infinite Fourier expansion is the Bochner–Fejér’s summation method, which was mentioned in the introduction of this article (and already used in Lemma 3.2).
$f_1(t)$
. This generalizes Proposition 3.1 for the case of a (nonnecessarily finite) arbitrary set of exponents. The main ingredient in order to prove this result for the case of functions with an infinite Fourier expansion is the Bochner–Fejér’s summation method, which was mentioned in the introduction of this article (and already used in Lemma 3.2).
Theorem 3.4 Let
![]() $\Lambda $
be a set of exponents,
$\Lambda $
be a set of exponents,
![]() $\mathcal {G}$
an equivalence class in
$\mathcal {G}$
an equivalence class in
 , and
, and
![]() $f_1,f_2\in \mathcal {G}$
. Fixed
$f_1,f_2\in \mathcal {G}$
. Fixed
![]() $\varepsilon>0$
, there exists a relatively dense set of real numbers
$\varepsilon>0$
, there exists a relatively dense set of real numbers
![]() $\{\tau \}$
such that
$\{\tau \}$
such that
Proof Let
![]() $f_1(t),f_2(t)\in AP(\mathbb {R},X)$
be two
$f_1(t),f_2(t)\in AP(\mathbb {R},X)$
be two
![]() $^*$
-equivalent almost periodic functions whose Fourier series are given by
$^*$
-equivalent almost periodic functions whose Fourier series are given by
 $\sum _{j\geq 1}a_je^{i\lambda _jt},\ a_j\in X$
, and
$\sum _{j\geq 1}a_je^{i\lambda _jt},\ a_j\in X$
, and
 $\sum _{j\geq 1}b_je^{i\lambda _jt},\ b_j\in X$
, respectively. Likewise, consider
$\sum _{j\geq 1}b_je^{i\lambda _jt},\ b_j\in X$
, respectively. Likewise, consider
 $P_N^{f_1}(t)=\sum _{m=1}^Nr_{m,N}a_me^{i\lambda _mt}$
and
$P_N^{f_1}(t)=\sum _{m=1}^Nr_{m,N}a_me^{i\lambda _mt}$
and
 $P_N^{f_2}(t)=\sum _{m=1}^Nr_{m,N}b_me^{i\lambda _mt}$
the (Bochner–Fejér’s) sequences of trigonometric polynomials associated with
$P_N^{f_2}(t)=\sum _{m=1}^Nr_{m,N}b_me^{i\lambda _mt}$
the (Bochner–Fejér’s) sequences of trigonometric polynomials associated with
![]() $f_1(t)$
and
$f_1(t)$
and
![]() $f_2(t)$
, respectively, where the rational numbers
$f_2(t)$
, respectively, where the rational numbers
![]() $r_{m,N}$
depend on m and N, but not on
$r_{m,N}$
depend on m and N, but not on
![]() $a_m$
and
$a_m$
and
![]() $b_m$
, and
$b_m$
, and
![]() $r_{m,k}\to 1$
as
$r_{m,k}\to 1$
as
![]() $k\to \infty $
. In this way, fixed
$k\to \infty $
. In this way, fixed
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $N_{\varepsilon }$
which satisfies the condition
$N_{\varepsilon }$
which satisfies the condition
 $$ \begin{align} \|f_1(t)-P_{N_{\varepsilon}}^{f_1}(t)\|<\varepsilon/3\ \ \ \mbox{and }\ \ \|f_2(t)-P_{N_{\varepsilon}}^{f_2}(t)\|<\varepsilon/3. \end{align} $$
$$ \begin{align} \|f_1(t)-P_{N_{\varepsilon}}^{f_1}(t)\|<\varepsilon/3\ \ \ \mbox{and }\ \ \|f_2(t)-P_{N_{\varepsilon}}^{f_2}(t)\|<\varepsilon/3. \end{align} $$
Furthermore, since
 $P_{N_{\varepsilon }}^{f_1}(t)$
and
$P_{N_{\varepsilon }}^{f_1}(t)$
and
 $P_{N_{\varepsilon }}^{f_2}(t)$
are
$P_{N_{\varepsilon }}^{f_2}(t)$
are
![]() $^*$
-equivalent (because
$^*$
-equivalent (because
![]() $f_1,f_2\in \mathcal {G}$
) by Proposition 3.1, there exists a relatively dense set of real numbers
$f_1,f_2\in \mathcal {G}$
) by Proposition 3.1, there exists a relatively dense set of real numbers
![]() $\{\tau \}$
such that
$\{\tau \}$
such that
 $$ \begin{align} \|P_{N_{\varepsilon}}^{f_1}(t+\tau)-P_{N_{\varepsilon}}^{f_2}(t)\|<\varepsilon/3\ \forall \tau\in\{\tau\}. \end{align} $$
$$ \begin{align} \|P_{N_{\varepsilon}}^{f_1}(t+\tau)-P_{N_{\varepsilon}}^{f_2}(t)\|<\varepsilon/3\ \forall \tau\in\{\tau\}. \end{align} $$
Consequently, from (3.2) and (3.3), we conclude for any
![]() $\tau \in \{\tau \}$
that
$\tau \in \{\tau \}$
that
 $$ \begin{align*}\|f_1(t+\tau)-f_2(t)\|\leq \|f_1-P_{N_{\varepsilon}}^{f_1}\|+\|P_{N_{\varepsilon}}^{f_1}(t+\tau)-P_{N_{\varepsilon}}^{f_2}(t)\|+\|P_{N_{\varepsilon}}^{f_2}-f_2\|<\varepsilon.\end{align*} $$
$$ \begin{align*}\|f_1(t+\tau)-f_2(t)\|\leq \|f_1-P_{N_{\varepsilon}}^{f_1}\|+\|P_{N_{\varepsilon}}^{f_1}(t+\tau)-P_{N_{\varepsilon}}^{f_2}(t)\|+\|P_{N_{\varepsilon}}^{f_2}-f_2\|<\varepsilon.\end{align*} $$
That is,
![]() $f_2(t)$
can be approximated by translates of
$f_2(t)$
can be approximated by translates of
![]() $f_1(t)$
. ▪
$f_1(t)$
. ▪
What is more, by taking Lemma 3.2 into account, Theorem 3.4 can be more generally stated as follows.
Corollary 3.5 Let
![]() $\Lambda =\{\lambda _1,\ldots ,\lambda _j,\ldots \}$
be a set of exponents and
$\Lambda =\{\lambda _1,\ldots ,\lambda _j,\ldots \}$
be a set of exponents and
![]() $f_1\in \mathcal {F}_{\Lambda }^X$
whose Fourier series is given by
$f_1\in \mathcal {F}_{\Lambda }^X$
whose Fourier series is given by
 $\sum _{j\geq 1}a_je^{i\lambda _jt},\ a_j\in X$
. Consider
$\sum _{j\geq 1}a_je^{i\lambda _jt},\ a_j\in X$
. Consider
![]() $b_j\in X$
such that
$b_j\in X$
such that
 $\sum _{j\geq 1}b_je^{i\lambda _jt}$
and
$\sum _{j\geq 1}b_je^{i\lambda _jt}$
and
 $\sum _{j\geq 1}a_je^{i\lambda _jt}$
are
$\sum _{j\geq 1}a_je^{i\lambda _jt}$
are
![]() $^*$
-equivalent. Fixed
$^*$
-equivalent. Fixed
![]() $\varepsilon>0$
, there exists a relatively dense set of real numbers
$\varepsilon>0$
, there exists a relatively dense set of real numbers
![]() $\{\tau \}$
such that
$\{\tau \}$
such that
where
![]() $f_2\in \mathcal {F}_{\Lambda }^X$
is an almost periodic function whose Fourier series is given by
$f_2\in \mathcal {F}_{\Lambda }^X$
is an almost periodic function whose Fourier series is given by
 $\sum _{j\geq 1}b_je^{i\lambda _jt}$
.
$\sum _{j\geq 1}b_je^{i\lambda _jt}$
.
The following result, which extends [Reference Sepulcre and Vidal16, Proposition 3], concerns the concept of convergence in
![]() $AP(\mathbb {R},X)$
. With respect to the topology of
$AP(\mathbb {R},X)$
. With respect to the topology of
![]() $AP(\mathbb {R},X)$
, it is satisfied that the equivalence classes of
$AP(\mathbb {R},X)$
, it is satisfied that the equivalence classes of
 are closed. In fact, more specifically, they are sequentially compact. The proof is based on Lemma 3.2, and it is analogous to that of [Reference Sepulcre and Vidal16, Proposition 3] (where the last statement is deduced from Helly’s selection principle).
are closed. In fact, more specifically, they are sequentially compact. The proof is based on Lemma 3.2, and it is analogous to that of [Reference Sepulcre and Vidal16, Proposition 3] (where the last statement is deduced from Helly’s selection principle).
Proposition 3.6 Let
![]() $\Lambda $
be a set of exponents and
$\Lambda $
be a set of exponents and
![]() $\mathcal {G}$
an equivalence class in
$\mathcal {G}$
an equivalence class in
 . Then
. Then
![]() $\mathcal {G}$
is sequentially compact.
$\mathcal {G}$
is sequentially compact.
Regarded as members of a metric space, sequential compactness is the same as compactness (in the topology induced by the metric), and it implies being closed. So, as a consequence of Proposition 3.6 and with respect to the topology of
![]() $AP(\mathbb {R},X)$
, we state that the family of translates of a function
$AP(\mathbb {R},X)$
, we state that the family of translates of a function
![]() $f\in \mathcal {F}_{\Lambda }^X$
is closed on its equivalence class of
$f\in \mathcal {F}_{\Lambda }^X$
is closed on its equivalence class of
 . In fact, this result can be improved in the sense that, fixed a function
. In fact, this result can be improved in the sense that, fixed a function
![]() $f\in \mathcal {F}_{\Lambda }^X$
, the limit points of the set of the translates
$f\in \mathcal {F}_{\Lambda }^X$
, the limit points of the set of the translates
![]() $\mathcal {T}_f=\{f(t+\tau ):\tau \in \mathbb {R}\}$
of f are precisely the almost periodic functions which are
$\mathcal {T}_f=\{f(t+\tau ):\tau \in \mathbb {R}\}$
of f are precisely the almost periodic functions which are
![]() $^*$
-equivalent to f. The proof is rather similar to that of [Reference Sepulcre and Vidal16, Theorem 2].
$^*$
-equivalent to f. The proof is rather similar to that of [Reference Sepulcre and Vidal16, Theorem 2].
Theorem 3.7 Let
![]() $\Lambda $
be a set of exponents,
$\Lambda $
be a set of exponents,
![]() $\mathcal {G}$
an equivalence class in
$\mathcal {G}$
an equivalence class in
 , and
, and
![]() $f\in \mathcal {G}$
. Then the set of functions
$f\in \mathcal {G}$
. Then the set of functions
![]() $\mathcal {T}_f=\{f_{\tau }(t):=f(t+\tau ):\tau \in \mathbb {R}\}$
is dense in
$\mathcal {T}_f=\{f_{\tau }(t):=f(t+\tau ):\tau \in \mathbb {R}\}$
is dense in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
We have seen in the introduction that the functions in
![]() $AP(\mathbb {R},X)$
satisfy the Bochner-type property consisting of the relative compactness of the set
$AP(\mathbb {R},X)$
satisfy the Bochner-type property consisting of the relative compactness of the set
![]() $\{f(t+\tau )\}$
,
$\{f(t+\tau )\}$
,
![]() $\tau \in \mathbb {R}$
, associated with an arbitrary function
$\tau \in \mathbb {R}$
, associated with an arbitrary function
![]() $f\in AP(\mathbb {R},X)$
. As an important consequence of Theorem 3.7, we have refined this property in the sense that we show that the condition of almost periodicity of a function
$f\in AP(\mathbb {R},X)$
. As an important consequence of Theorem 3.7, we have refined this property in the sense that we show that the condition of almost periodicity of a function
![]() $f(t)\in AP(\mathbb {R},X)$
yields that every sequence
$f(t)\in AP(\mathbb {R},X)$
yields that every sequence
![]() $\{f(t+\tau _n)\}$
,
$\{f(t+\tau _n)\}$
,
![]() $\tau _n\in \mathbb {R}$
, of translates of f has a subsequence that converges with the topology of
$\tau _n\in \mathbb {R}$
, of translates of f has a subsequence that converges with the topology of
![]() $AP(\mathbb {R},X)$
to a function which is
$AP(\mathbb {R},X)$
to a function which is
![]() $^*$
-equivalent to f.
$^*$
-equivalent to f.
Corollary 3.8 Let
![]() $f\in \mathcal {A}(\mathbb {R},X)$
. Then f is in
$f\in \mathcal {A}(\mathbb {R},X)$
. Then f is in
![]() $AP(\mathbb {R},X)$
if and only if the closure of its set of translates is compact. Furthermore, in this case, this closure coincides with its equivalence class.
$AP(\mathbb {R},X)$
if and only if the closure of its set of translates is compact. Furthermore, in this case, this closure coincides with its equivalence class.