Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T05:54:16.628Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Covering by Convex Bodies

Published online by Cambridge University Press:  20 November 2018

Gábor Fejes Tóth
Gábor Fejes Tóth*
Affiliation:
Rényi Institute of Mathematics, Hungarian Academy of Sciences, Pf. 127, H-1364 Budapest, Hungary e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A classical theorem of Rogers states that for any convex body 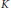$K$ in $n$-dimensional Euclidean space there exists a covering of the space by translates of 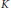$K$ with density not exceeding 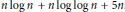$n\,\log \,n\,+\,n\,\log \,\log \,n\,+\,5$. Rogers’ theorem does not say anything about the structure of such a covering. We show that for sufficiently large values of $n$ the same bound can be attained by a covering which is the union of 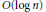$O\left( \log \,n \right)$ translates of a lattice arrangement of 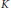$K$.

Keywords

52C0752C1711H31
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 361 - 365
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Erdős, P. and Rogers, C. A., Covering space with convex bodies. Acta Arithmetica 7(1962), 281–285.Google Scholar
[2] Füredi, Z. and Kang, J.-H., Covering the n-space by convex bodies and its chromatic number. Discrete Math. 308(2008), 4495–4500 Google Scholar
[3] Rogers, C. A., A note on coverings. Mathematika 4(1957), 1–6.Google Scholar
[4] Rogers, C. A., Lattice coverings of space: the Minkowski–Hlawka theorem. Proc. London Math. Soc. 8(1958), 447–465.Google Scholar
[5] Rogers, C. A., Lattice coverings of space. Mathematika 6(1959), 33–39.Google Scholar
[6] Schmidt, W., Masstheorie in der Geometrie der Zahlen. Acta Mathematica 102(1959), 159–224.Google Scholar
[7] Siegel, C. L., A mean value theorem in geometry of numbers. Ann. of Math. 46(1945), 340–347.Google Scholar