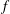Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T01:59:47.812Z Has data issue: false hasContentIssue false
  • English
  • Français

Newton Complementary Duals of $f$-Ideals

Part of: Algebraic combinatorics Arithmetic rings and other special rings

Published online by Cambridge University Press:  15 October 2018

Samuel Budd  and
Adam Van Tuyl
Samuel Budd
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, ON, L8S 4L8 Email: [email protected]@[email protected]
Adam Van Tuyl
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, ON, L8S 4L8 Email: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A square-free monomial ideal 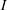$I$ of 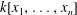$k[x_{1},\ldots ,x_{n}]$ is said to be an 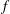$f$-ideal if the facet complex and non-face complex associated with 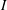$I$ have the same 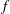$f$-vector. We show that 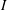$I$ is an 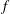$f$-ideal if and only if its Newton complementary dual 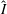$\widehat{I}$ is also an 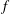$f$-ideal. Because of this duality, previous results about some classes of 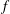$f$-ideals can be extended to a much larger class of 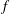$f$-ideals. An interesting by-product of our work is an alternative formulation of the Kruskal–Katona theorem for 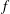$f$-vectors of simplicial complexes.

Keywords

f-idealsfacet idealStanley–Reisner correspondencef-vectorsNewton complementary dualKruskal–Katona

MSC classification

Primary: 05E45: Combinatorial aspects of simplicial complexes
Secondary: 05E40: Combinatorial aspects of commutative algebra 13F55: Stanley-Reisner face rings; simplicial complexes
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 231 - 241
Copyright
© Canadian Mathematical Society 2018 

Footnotes

1

Current address for Budd: 2061 Oliver Road, Thunder Bay, ON, P7G 1P7

Parts of this paper appeared in the first author’s MSc project [4]. The second author’s research was supported in part by NSERC Discovery Grant 2014-03898.

References

Abbasi, G. Q., Ahmad, S., Anwar, I., and Baig, W. A., f-Ideals of degree 2 . Algebra Colloq. 19(2012), 921–926. https://doi.org/10.1142/S10053867100788.Google Scholar
Ansaldi, K., Lin, K., and Shen, Y., Generalized Newton complementary duals of monomial ideals. 2017. arxiv:1702.00519v1.Google Scholar
Anwar, I., Mahmood, H., Binyamin, M. A., and Zafar, M. K., On the characterization of f-ideals . Comm. Algebra 42(2014), 3736–3741. https://doi.org/10.1080/00927872.2013.792092.Google Scholar
Budd, S., An introduction to $f$ -ideals and their complements. MSc Project, McMaster University, Hamilton, Canada, 2017.Google Scholar
Costa, B. and Simis, A., New constructions of Cremona maps . Math. Res. Lett. 20(2013), 629–645. https://doi.org/10.4310/MRL.2013.v20.n4.a3.Google Scholar
Dória, A. and Simis, A., The Newton complementary dual revisited . J. Algebra Appl. 17(2018), 1850004, 16 pp. https://doi.org/10.1142/S0219498818500044.Google Scholar
Faridi, S., The facet ideal of a simplicial complex . Manuscripta Math. 109(2002), 159–174. https://doi.org/10.1007/s00229-002-0293-9.Google Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Guo, J., Wu, T., and Liu, Q., F-Ideals and f-graphs . Comm. Algebra 45(2016), 3207–3220.Google Scholar
Guo, J. and Wu, T., On the (n, d) th  f-ideals . J. Korean Math. Soc. 52(2015), 685–697. https://doi.org/10.4134/JKMS.2015.52.4.685.Google Scholar
Herzog, J. and Hibi, T., Monomial ideals, Graduate Texts in Mathematics, 260, Springer-Verlag, London, 2011. https://doi.org/10.1007/978-0-85729-106-6.Google Scholar
Katona, G., A theorem of finite sets . Theory of graphs (Proc. Colloq., Tihany, 1966). Academic Press, New York, 1968, pp. 187–207.Google Scholar
Kruskal, J. B., The number of simplices in a complex . Mathematical optimization techniques. Univ. of California Press, Berkeley, Calif, 1963, pp. 251–278.Google Scholar
Mahmood, H., Anwar, I., and Zafar, M. K., A construction of Cohen–Macaulay f-graphs . J. Algebra Appl. 13(2014), 1450012, 7 pp. https://doi.org/10.1142/S0219498814500121.Google Scholar
Mahmood, H., Anwar, I., Binyamin, M. A., and Yasmeen, S., On the connectedness of f-simplicial complexes . J. Algebra Appl. 16(2017), 1750017, 9 pp. https://doi.org/10.1142/S0219498817500177.Google Scholar