Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lin, Yi Jie
and
Zhou, Jian
2017.
Topological recursion relations from Pixton relations.
Acta Mathematica Sinica, English Series,
Vol. 33,
Issue. 4,
p.
470.


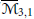 via the Invariance Constraint
via the Invariance Constraint