Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T13:41:38.765Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Approach to Operator Spaces

Published online by Cambridge University Press:  20 November 2018

Edward G. Effros  and
Zhong-Jin Ruan
Edward G. Effros
Affiliation:
Mathematics Department, UCLA, Los Angeles, CA 90024
Zhong-Jin Ruan
Affiliation:
Mathematics Department, University of Illinois, Urbana, IL 61801
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

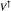The authors previously observed that the space of completely bounded maps between two operator spaces can be realized as an operator space. In particular, with the appropriate matricial norms the dual of an operator space V is completely isometric to a linear space of operators. This approach to duality enables one to formulate new analogues of Banach space concepts and results. In particular, there is an operator space version ⊗μ of the Banach space projective tensor product 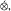, which satisfies the expected functorial properties. As is the case for Banach spaces, given an operator space V, the functor W |—> V ⊗μ W preserves inclusions if and only if 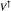is an injective operator space.

Keywords

46L05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 34 , Issue 3 , 01 September 1991 , pp. 329 - 337
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Blecher, D. and Paulsen, V., Tensor products of operator spaces , preprint.Google Scholar
2. Blecher, D., Z.-J. Ruan and Sinclair, A., A characterization of operator algebras, J. Funct. Anal. 89 (1990), 188–201.Google Scholar
3. Choi, M.-D., Non-linear completely bounded maps, unpub. note.Google Scholar
4. Christensen, E., E. Effros and Sinclair, A., Completely bounded multilinear maps and C*-algebraic cohomology, Inv. Math. 90 (1987), 279–296.Google Scholar
5. Christensen, E. and Sinclair, A., Representations of completely bounded multilinear operators, J. Funct. Anal. 72 (1987), 151–181. 6 , On the Hochschild cohomology for von Neumann algebras, to appear.Google Scholar
7. Effros, E., Advances in quantized functional analysis. Proceedings of the International Congress of Mathematicians, Berkeley, 1986.Google Scholar
8. Effros, E. and Ruan, Z.-J., On matricially normed spaces, Pac. J. Math. 132 (1988), 243–264.Google Scholar
9. Effros, E. and Ruan, Z.-J., Representations of operator bimodules and their applications , J. Operator Theory 19( 1988), 137– 157.Google Scholar
10. Effros, E. and Ruan, Z.-J., Multivariate multipliers for groups and their operator algebras , Proc. Symp. Pure Math. 51 (1990), parti.Google Scholar
11. Grothendieck, A., Une caracterisation vectorielle-métrique des espaces L1, Canadian J. Math. 7 (1955), 552–561.Google Scholar
12. Haagerup, U., Group C* -algebras without the completely bounded approximation property, to appear.Google Scholar
13. Itoh, T., On the completely bounded map of a C*-algebra to its dual space, Bull. London Math. Soc. 19 (1987), 546–550.Google Scholar
14. Paulsen, V. and Smith, R., Multilinear maps and tensor norms on operator systems, J. Funct. Anal. 73 (1987), 258–276.Google Scholar
15. Ruan, Z.-J., Subspaces of C*-algebras, J. Funct. Anal. 76 (1988), 217–230.Google Scholar
16. Ruan, Z.-J., On matricially normed spaces associated with operator algebras. Ph.D. Dissertation, UCLA, 1987.Google Scholar
17. Smith, R., Completely bounded maps between C -algebras, J. London Math Soc. (2)27 (1983), 157–166.Google Scholar