Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T18:05:33.011Z Has data issue: false hasContentIssue false
  • English
  • Français

A Multiple Sequence Ergodic Theorem

Published online by Cambridge University Press:  20 November 2018

James H. Olsen
James H. Olsen*
Affiliation:
North Dakota State University
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 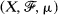be a σ-finite measure space, {T1, …, Tk} a set of linear operators of 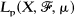, some p, 1≤p≤∞.If

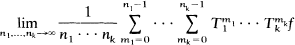
exists a.e. for all f ∊ Lp, we say that the multiple sequence ergodic theorem holds for {T1, …, Tk}. If f≥0 implies Tf≥0, we say that T is positive. If there exists an operator S such that |Tf(x)|≥S |f|(x) a.e., we say that T is dominated by S. In this paper we prove that if T1, …, Tk are dominated by positive contractions of 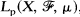, p fixed, 1<p<∞, then the multiple sequence ergodic theorem holds for {T1, …, Tk}.

Keywords

47A3528A65
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 4 , 01 December 1983 , pp. 493 - 497
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Akcoglu, M. A., A pointwise ergodic theorem in Lp spaces, Can. J. Math 27 (1975), 1975- 1982.Google Scholar
2. Dunford, N. and Schwartz, J., Linear Operators I, John Wiley, New York, 1958.Google Scholar
3. Halmos, P. R., Lectures on Ergodic Theory, Mathematical Society of Japan, Tokyo, 1956.Google Scholar
4. Kan, C., Ergodic properties of Lamperti operators, Can. J. Math 30 (1978), 1206-1214.Google Scholar
5. Lorch, E., Spectral Theory, Oxford University Press, New York, 1962.Google Scholar
6. Sato, R., Individual ergodic theorems for commuting operators, to appear.Google Scholar