Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T12:00:55.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Multidimensional Exponential Inequalities with Weights

Published online by Cambridge University Press:  20 November 2018

Dah-Chin Luor
Dah-Chin Luor*
Affiliation:
Department of Applied Mathematics, I-Shou University, Ta-Hsu, Kaohsiung 84008, Taiwan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish sufficient conditions on the weight functions $u$ and $v$ for the validity of the multidimensional weighted inequality

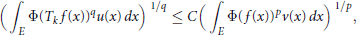$${{\left( \int_{E}{\Phi {{\left( {{T}_{k}}f\left( x \right) \right)}^{q}}u\left( x \right)dx} \right)}^{1/q}}\,\le \,C{{\left( \int_{E}{\Phi {{\left( f\left( x \right) \right)}^{p}}v\left( x \right)dx} \right)}^{1/p}},$$

where 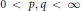$0\,<\,p,\,q\,<\,\infty $, 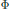$\Phi $ is a logarithmically convex function, and 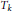${{T}_{k}}$ is an integral operator over star-shaped regions. The condition is also necessary for the exponential integral inequality. Moreover, the estimation of 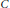$C$ is given and we apply the obtained results to generalize some multidimensional Levin–Cochran-Lee type inequalities.

Keywords

26D1526D10multidimensional inequalitiesgeometric mean operatorsexponential inequalitiesstar-shaped regions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 327 - 339
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Andrews, G. E., Askey, R., and Roy, R., Special Functions. Encyclopedia of Mathematics and its Applications 71. Cambridge University Press, Cambridge, 1999.Google Scholar
[2] Čižmešija, A. and Pečarić, J., Some new generalisations of inequalities of Hardy and Levin-Cochran-Lee. Bull. Austral. Math. Soc. 63(2001), no. 1, 105–113. doi:10.1017/S000497270001916XGoogle Scholar
[3] Čižmešija, A., Pečarić, J., and Perić, I., Mixed means and inequalities of Hardy and Levin-Cochran-Lee type for multidimensional balls. Proc. Amer. Math. Soc. 128(2000), no. 9, 2543–2552. doi:10.1090/S0002-9939-99-05408-8Google Scholar
[4] Cochran, J. A. and Lee, C.-S., Inequalities related to Hardy's and Heinig’s. Math. Proc. Cambridge Philos. Soc. 96(1984), no. 1, 1–7. doi:10.1017/S0305004100061879Google Scholar
[5] Drábek, P., Heinig, H. P., and Kufner, A., Higher dimensional Hardy inequality. In: General Inequalities, 7. Internat. Ser. Num. Math. 123. Birkhäuser, Basel, 1997, pp. 3–16.Google Scholar
[6] Gupta, B., Jain, P., Persson, L.-E., and Wedestig, A., Weighted geometric mean inequalities over cones in ℝ n . J. Inequal. Pure Appl. Math. 4(2003), Article 68.Google Scholar
[7] Hardy, G. H., Littlewood, J. E., and Pólya, G., Inequalities. Second edition. Cambridge, at the University Press, 1952.Google Scholar
[8] Heinig, H. P., Weighted inequalities in Fourier analysis. In: Nonlinear Analysis, Function Spaces and Applications, Vol. 4. Teubner-Texte Math. 119. Teubner, Leipzig, 1990, pp. 42–85.Google Scholar
[9] Heinig, H. P., Modular inequalities for the Hardy averaging operator. Math. Bohem. 124(1999), no. 2–3, 231–244.Google Scholar
[10] Heinig, H. P., Exponential inequalities for a class of operators. Int. J. Math. Math. Sci. 31(2002), no. 5, 283–290. doi:10.1155/S0161171202112245Google Scholar
[11] Heinig, H. P., Kerman, R., and Krbec, M., Weighted exponential inequalities. Georgian Math. J. 8(2001), no. 1, 69–86.Google Scholar
[12] Jain, P., Persson, L.-E., and Singh, A. P., On geometric mean inequalities with exponential weights. Soochow J. Math. 30(2004), no. 4, 391–400.Google Scholar
[13] Jain, P., Persson, L.-E., and Wedestig, A., Carleman-Knopp type inequalities via Hardy inequalities. Math. Inequal. Appl. 4(2001), no. 3, 343–355.Google Scholar
[14] Jain, P., Persson, L.-E., and Wedestig, A., Multidimensional Cochran and Lee type inequalities with weights. Proc. A. Razmadze Math. Inst. 129(2002), 17–27.Google Scholar
[15] Jain, P. and Singh, A. P., A characterization for the boundedness of geometric mean operator. Appl. Math. Lett. 13(2000), no. 8, 63–67. doi:10.1016/S0893-9659(00)00097-5Google Scholar
[16] Jarrah, A. M. and Singh, A. P., A limiting case of Hardy's inequality. Indian J. Math. 43(2001), no. 1, 21–36.Google Scholar
[17] Kaijser, S., Nikolova, L., Persson, L.-E., and Wedestig, A., Hardy-type inequalities via convexity. Math. Inequal. Appl. 8(2005), no. 3, 403–417.Google Scholar
[18] Levinson, N., Generalizations of an inequality of Hardy. Duke Math. J. 31(1964), 389–394. doi:10.1215/S0012-7094-64-03137-0Google Scholar
[19] Love, E. R., Inequalities related to those of Hardy and of Cochran and Lee. Math. Proc. Cambridge Philos. Soc. 99(1986), no. 3, 395–408. doi:10.1017/S0305004100064343Google Scholar
[20] Love, E. R., Inequalities related to Knopp's inequality. J. Math. Anal. Appl. 137(1989), no. 1, 173–180. doi:10.1016/0022-247X(89)90281-3Google Scholar
[21] Opic, B. and Gurka, P., Weighted inequalities for geometric means. Proc. Amer. Math. Soc. 120(1994), no. 3, 771–779. doi:10.2307/2160469Google Scholar
[22] Opic, B. and Kufner, A., Hardy-type inequalities. Pitman Research Notes in Mathematics Series 219. Longman Scientific & Technical, Harlow, 1990.Google Scholar
[23] Persson, L.-E. and Stepanov, V D., Weighted integral inequalities with the geometric mean operator. J. Inequal. Appl. 7(2002), no. 5, 727–746. doi:10.1155/S1025583402000371Google Scholar
[24] Pick, L. and Opic, B., On the geometric mean operator. J. Math. Anal. Appl. 183(1994), no. 3, 652–662. doi:10.1006/jmaa.1994.1172Google Scholar
[25] Sinnamon, G., Weighted Hardy and Opial-type inequalities. J. Math. Anal. Appl. 160(1991), no. 2, 434–445. doi:10.1016/0022-247X(91)90316-RGoogle Scholar
[26] Sinnamon, G., One-dimensional Hardy-type inequalities in many dimensions. Proc. Roy. Soc. Edinburgh Sect. A 128(1998), no. 4, 833–848.Google Scholar