Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T12:49:15.221Z Has data issue: false hasContentIssue false
  • English
  • Français

Moduli Spaces of Polygons and Punctured Riemann Spheres

Published online by Cambridge University Press:  20 November 2018

Philip Foth
Philip Foth*
Affiliation:
Department of Mathematics University of Arizona Tucson, AZ 85721-0089, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this note is to give a simple combinatorial construction of the map from the canonically compactified moduli spaces of punctured complex projective lines to the moduli spaces 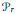${{P}_{r}}$ of polygons with fixed side lengths in the Euclidean space 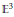${{\mathbb{E}}^{3}}$. The advantage of this construction is that one can obtain a complete set of linear relations among the cycles that generate homology of 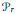${{P}_{r}}$. We also classify moduli spaces of pentagons.

Keywords

14D2018G5514H10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 2 , 01 June 2000 , pp. 162 - 173
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Beilinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers. Analyse et topologie sur les espaces singuliers, Astérisque 100(1982), 5–171.Google Scholar
[2] Deligne, P. and Mostow, G. D., Monodromy of hypergeometric functions and non-lattice integral monodromy. Inst. Hautes E´ tudes Sci. Publ. Math. 63(1986), 5–90.Google Scholar
[3] Getzler, E., Operads and moduli spaces of genus 0 Riemann surfaces. Themoduli space of curves (Texel Island, 1994), Progr.Math. 129, Birkhauser, Boston, MA, 1995, 199–230.Google Scholar
[4] Hausmann, J.-C., Sur la topologie des bras articulés. Algebraic Topology (Poznan, 1989), Springer Lecture Notes in Math. 1474(1989), 146–159.Google Scholar
[5] Hausmann, J.-C. and Knutson, A., The cohomology ring of polygon spaces. Ann. Inst. Fourier 48(1998), 281–321.Google Scholar
[6] Hu, Y., Moduli spaces of stable polygons and symplectic structures on M0, n. Composito Math., to appear.Google Scholar
[7] Kapovich, M. and Millson, J., The symplectic geometry of polygons in Euclidean space. Diff, J.. Geom. 44(1996), 479–513.Google Scholar
[8] Kapranov, M. M., Chow quotients of Grassmanians I. M, I.. Gelfand Seminar, Adv. Soviet Math. 16(1993), 29–110.Google Scholar
[9] Keel, S., Intersection theory of moduli space of stable N-pointed curves of genus zero. Trans. Amer. Math. Soc. (2) 330(1992), 545–574.Google Scholar
[10] Klyachko, A. A., Spatial polygons and stable configurations of points in the projective line. In: Algebraic geometry and its applications (Yaroslavl, 1992), Aspects Math. E25, Vieweg, Braunschweig, 1994, 67–84.Google Scholar
[11] Knudsen, F., The projectivity of the moduli space of stable curves, II: the stacks Mg, n. Math. Scand. 52(1983), 161–199.Google Scholar
[12] Kontsevich, M. and Manin, Yu., Gromov-Witten classes, quantum cohomology, and enumerative geometry. Comm. Math. Phys. 164(1994), 525–562.Google Scholar