Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T15:37:11.012Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean Value Theorem for the m-Integral of Dinculeanu

Published online by Cambridge University Press:  20 November 2018

Pedro Morales
Pedro Morales*
Affiliation:
Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical mean value theorem asserts that if f is a real, bounded, Riemann integrable function defined on a finite real interval a≤t≤b, then 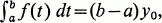, where infa≤t≤bf(t)≤y0supa≤t≤bf(t). The extensions of Choquet [3], Price [15], and of this paper generalize the fact that y0 belongs to the closure of the convex hull of f([a, b]). The version of Choquet ([3, p. 38]) applies to a continuous function on a compact interval with values in a Banach space; that of Price ([15, p. 24]) applies to a bilinear integral of a special type containing the Birkhoff integral [2]. The m-integral of Dinculeanu [6] (specialization of Bartle's *- integral [1]) leaves intact the Lebesgue dominated convergence theorem and is strong enough to support an extended development. The paper is organized as follows: the object of §2 is to express the integral of a bounded m-integrable function as a limit of Riemann sums; §3 gives Price's generalization of "convex hull" [15]; the theorem of the paper is established in §4; §5 gives applications to vector differentiation which, for continuously differentiable functions, contain results of Dieudonné [5] and McLeod [13].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 2 , June 1972 , pp. 243 - 251
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Bartle, R., A general bilinear vector integral, Studia Math. 15 (1956), 337-352.Google Scholar
2. Birkhoff, G., Integration of functions with values in a Banach space, Trans. Amer. Math. Soc. 38 (1935), 357-378.Google Scholar
3. Choquet, M., Equations différentielles, Centre de Documentation Universitaire, Paris, 1961.Google Scholar
4. Dantzer, L., Grunbaum, B. and Klee, V., Helly's theorem and its relatives, Proc. Sympos. Pure Math. Vol. VII (convexity), Amer. Math. Soc. (1963), 101-180.Google Scholar
5. Dieudonné, J., Foundations of modem analysis, Academic Press, New York, 1960.Google Scholar
6. Dinculeanu, N., Vector measures, Pergamon Press, New York, 1967.Google Scholar
7. Dotson, W. Jr, A note on complex polynomials having Rollers property and the mean value property for derivatives, Math. Mag. (3) 41 (1968), 140-144.Google Scholar
8. Dunford, N. and Schwartz, J., Linear operators, Part I, Interscience, New York, 1964.Google Scholar
9. Graves, L., Riemann integration and Taylor theorem in general analysis, Trans. Amer. Math. Soc. 29 (1927), 163-177.Google Scholar
10. Hanner, O., Connectedness and convex hulls, Seminar on convex sets, Inst, for Advanced Study, Princeton, N.J., (1949-50), 35-40.Google Scholar
11. Hildebrandt, T., Integration in abstract spaces, Bull. Amer. Math. Soc. 59 (1953), 111-139.Google Scholar
12. Lang, S., Analysis I, Addison-Wesley, Reading, Mass., 1968.Google Scholar
13. McLeod, R., Mean value theorem for vector valued functions, Proc. Edinburgh Math. Soc. (2) 14 (1965), 197-209.Google Scholar
14. McShane, E. and Botts, T., Real analysis, Van Nostrand, Princeton, N.J., 1959.Google Scholar
15. Price, G., The theory of integration, Trans. Amer. Math. Soc. 47 (1940), 1-50.Google Scholar