No CrossRef data available.
Published online by Cambridge University Press: 29 May 2023
Let 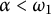 $\alpha < \omega _1$ be a prime component, and let
$\alpha < \omega _1$ be a prime component, and let 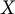 $X$ and
$X$ and 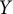 $Y$ be metric spaces. In [8], it was shown that if
$Y$ be metric spaces. In [8], it was shown that if 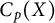 $C_p(X)$ and
$C_p(X)$ and 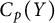 $C_p(Y)$ are linearly homeomorphic, then the scattered heights
$C_p(Y)$ are linearly homeomorphic, then the scattered heights 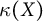 $\kappa (X)$ and
$\kappa (X)$ and 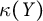 $\kappa (Y)$ of
$\kappa (Y)$ of 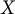 $X$ and
$X$ and 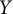 $Y$ satisfy
$Y$ satisfy 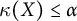 $\kappa (X) \leq \alpha $ if and only if
$\kappa (X) \leq \alpha $ if and only if 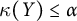 $\kappa (Y) \leq \alpha $. We will prove that this also holds if
$\kappa (Y) \leq \alpha $. We will prove that this also holds if 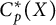 $C_p^*(X)$ and
$C_p^*(X)$ and 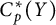 $C_p^*(Y)$ are linearly homeomorphic and that these results do not hold for arbitrary Tychonov spaces. We will also prove that if
$C_p^*(Y)$ are linearly homeomorphic and that these results do not hold for arbitrary Tychonov spaces. We will also prove that if 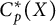 $C_p^*(X)$ and
$C_p^*(X)$ and 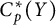 $C_p^*(Y)$ are linearly homeomorphic, then
$C_p^*(Y)$ are linearly homeomorphic, then 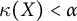 $\kappa (X) < \alpha $ if and only if
$\kappa (X) < \alpha $ if and only if 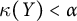 $\kappa (Y) < \alpha $, which was shown in [9] for
$\kappa (Y) < \alpha $, which was shown in [9] for 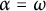 $\alpha = \omega $. This last statement is not always true for linearly homeomorphic
$\alpha = \omega $. This last statement is not always true for linearly homeomorphic 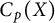 $C_p(X)$ and
$C_p(X)$ and 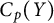 $C_p(Y)$. We will show that if
$C_p(Y)$. We will show that if 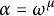 $\alpha = \omega ^{\mu }$ where
$\alpha = \omega ^{\mu }$ where 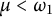 $\mu < \omega _1$ is a successor ordinal, it is true, but for all other prime components, this is not the case. Finally, we will prove that if
$\mu < \omega _1$ is a successor ordinal, it is true, but for all other prime components, this is not the case. Finally, we will prove that if 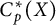 $C_p^*(X)$ and
$C_p^*(X)$ and 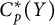 $C_p^*(Y)$ are linearly homeomorphic, then
$C_p^*(Y)$ are linearly homeomorphic, then 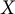 $X$ is scattered if and only if
$X$ is scattered if and only if 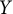 $Y$ is scattered. This result does not directly follow from the above results. We will clarify why the results for linearly homeomorphic spaces
$Y$ is scattered. This result does not directly follow from the above results. We will clarify why the results for linearly homeomorphic spaces 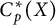 $C_p^*(X)$ and
$C_p^*(X)$ and 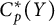 $C_p^*(Y)$ do require a different and more complex approach than the one that was used for linearly homeomorphic spaces
$C_p^*(Y)$ do require a different and more complex approach than the one that was used for linearly homeomorphic spaces 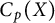 $C_p(X)$ and
$C_p(X)$ and 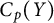 $C_p(Y)$.
$C_p(Y)$.