Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T16:15:04.045Z Has data issue: false hasContentIssue false
  • English
  • Français

A Künneth Theorem for p-Adic Groups

Published online by Cambridge University Press:  20 November 2018

A. Raghuram
A. Raghuram*
Affiliation:
Department of Mathematics, Oklahoma State University, Stillwater, OK 74078, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 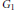${{G}_{1}}$ and 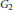${{G}_{2}}$ be 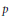$p$-adic groups. We describe a decomposition of Ext-groups in the category of smooth representations of 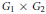${{G}_{1}}\times {{G}_{2}}$ in terms of Ext-groups for 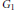${{G}_{1}}$ and 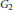${{G}_{2}}$. We comment on 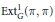$\text{Ext}_{G}^{1}\left( \pi ,\pi \right)$ for a supercuspidal representation 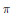$\pi$ of a 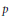$p$-adic group 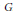$G$. We also consider an example of identifying the class, in a suitable 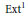$E\text{x}{{\text{t}}^{1}}$, of a Jacquet module of certain representations of 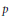$p$-adic 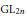$\text{G}{{\text{L}}_{2n}}$.

Keywords

22E5018G1555U25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 440 - 446
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Bernstein, J. N., Le “centre” de Bernstein. In: Reprsentations des groupes rductifs sur un corps local, Travaux en Cours, Hermann, Paris, 1984, pp. 1–32.Google Scholar
[2] Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups. Second edition. Mathematical Surveys and Monographs 67, American Mathematical Society, Providence, RI, 2000.Google Scholar
[3] Bushnell, C. J. and Kutzko, P. C., Smooth representations of reductive p-adic groups: structure theory via types. Proc. LondonMath. Soc. 77(1998), no. 3, 582–634.Google Scholar
[4] MacLane, S., Homology. Reprint of the 1975 edition. Classics in Mathematics. Springer-Verlag, Berlin, 1995.Google Scholar
[5] Raghuram, A., On the restriction to D* × D* of representations of p-adic GL2(D). To appear in the Canad. J. Math.Google Scholar