Kneser’s theorem in 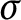$\sigma $-finite abelian groups

Abstract

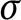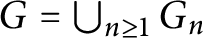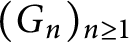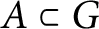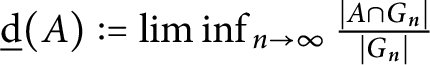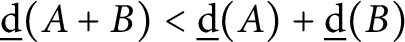Let G be a $\sigma $ -finite abelian group, i.e., $G=\bigcup _{n\geq 1} G_n$ where $(G_n)_{n\geq 1}$ is a nondecreasing sequence of finite subgroups. For any $A\subset G$ , let $\underline {\mathrm {d}}( A ):=\liminf _{n\to \infty }\frac {|A\cap G_n|}{|G_n|}$ be its lower asymptotic density. We show that for any subsets A and B of G, whenever $\underline {\mathrm {d}}( A+B )<\underline {\mathrm {d}}( A )+\underline {\mathrm {d}}( B )$ , the sumset 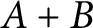$A+B$ must be periodic, that is, a union of translates of a subgroup 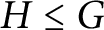$H\leq G$ of finite index. This is exactly analogous to Kneser’s theorem regarding the density of infinite sets of integers. Further, we show similar statements for the upper asymptotic density in the case where 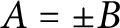$A=\pm B$ . An analagous statement had already been proven by Griesmer in the very general context of countable abelian groups, but the present paper provides a much simpler argument specifically tailored for the setting of 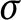$\sigma $ -finite abelian groups. This argument relies on an appeal to another theorem of Kneser, namely the one regarding finite sumsets in an abelian group.