Article contents
The intersection theory of the moduli stack of vector bundles on 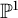 $\mathbb {P}^1$
$\mathbb {P}^1$
Published online by Cambridge University Press: 07 July 2022
Abstract
We determine the integral Chow and cohomology rings of the moduli stack
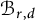 $\mathcal {B}_{r,d}$
of rank r, degree d vector bundles on
$\mathcal {B}_{r,d}$
of rank r, degree d vector bundles on
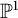 $\mathbb {P}^1$
-bundles. We work over a field k of arbitrary characteristic. We first show that the rational Chow ring
$\mathbb {P}^1$
-bundles. We work over a field k of arbitrary characteristic. We first show that the rational Chow ring
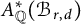 $A_{\mathbb {Q}}^*(\mathcal {B}_{r,d})$
is a free
$A_{\mathbb {Q}}^*(\mathcal {B}_{r,d})$
is a free
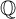 $\mathbb {Q}$
-algebra on
$\mathbb {Q}$
-algebra on
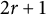 $2r+1$
generators. The isomorphism class of this ring happens to be independent of d. Then, we prove that the integral Chow ring
$2r+1$
generators. The isomorphism class of this ring happens to be independent of d. Then, we prove that the integral Chow ring
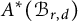 $A^*(\mathcal {B}_{r,d})$
is torsion-free and provide multiplicative generators for
$A^*(\mathcal {B}_{r,d})$
is torsion-free and provide multiplicative generators for
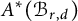 $A^*(\mathcal {B}_{r,d})$
as a subring of
$A^*(\mathcal {B}_{r,d})$
as a subring of
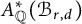 $A_{\mathbb {Q}}^*(\mathcal {B}_{r,d})$
. From this description, we see that
$A_{\mathbb {Q}}^*(\mathcal {B}_{r,d})$
. From this description, we see that
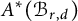 $A^*(\mathcal {B}_{r,d})$
is not finitely generated as a
$A^*(\mathcal {B}_{r,d})$
is not finitely generated as a
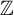 $\mathbb {Z}$
-algebra. Finally, when
$\mathbb {Z}$
-algebra. Finally, when
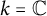 $k = \mathbb {C}$
, the cohomology ring of
$k = \mathbb {C}$
, the cohomology ring of
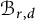 $\mathcal {B}_{r,d}$
is isomorphic to its Chow ring.
$\mathcal {B}_{r,d}$
is isomorphic to its Chow ring.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
During the preparation of this article, the author was supported by the Hertz Foundation and NSF GRFP under Grant No. DGE-1656518.
References
- 2
- Cited by



