Infinite Dimensional DeWitt Supergroups and their Bodies

Abstract

For Dewitt super groups $G$ modeled via an underlying finitely generated Grassmann algebra it is well known that when there exists a body group 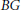$BG$ compatible with the group operation on $G$, then, generically, the kernel 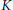$K$ of the body homomorphism is nilpotent. This is not true when the underlying Grassmann algebra is infinitely generated. We show that it is quasi-nilpotent in the sense that as a Banach Lie group its Lie algebra $\kappa$ has the property that for each 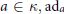$a\,\in \,\kappa ,\,\text{a}{{\text{d}}_{a}}$ has a zero spectrum. We also show that the exponential mapping from $\kappa$ to 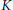$K$ is surjective and that 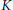$K$ is a quotient manifold of the Banach space $\kappa$ via a lattice in $\kappa$.