Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-02T07:12:07.297Z Has data issue: false hasContentIssue false
  • English
  • Français

The Group of the Quadratic Residue Tournament

Published online by Cambridge University Press:  20 November 2018

Myron Goldberg
Myron Goldberg*
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

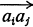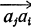A tournament Tn is a set of n nodes a1a2, …, an such that every pair (ai, aj) of distinct nodes is joined by exactly one of the oriented edges or . If 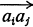is in Tn, then we say that ai dominates aj and write ai → aj.

The (automorphism) group G(Tn) of a tournament Tn is the group of all permutations ϕ of the nodes of Tn such that ϕ(a)→ϕ(b) if and only if a → b. It is known [9] that there exist tournaments whose group is abstractly isomorphic to a given group H if and only if H has odd order; thus all tournament groups are solvable, by the Feit-Thompson Theorem [7].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 1 , March 1970 , pp. 51 - 54
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Alspach, B., Goldberg, M. and Moon, J. W., The group of the composition of two tournaments, Math. Magazine 41 (1968), 77-90.Google Scholar
2. Assmus, E. F. Jr. and Mattson, H. F. Jr., Research to develop the algebraic theory of codes. AFCRL-68-0478, Scientific Report, Air Force Cambridge Research Laboratory, Bedford, Mass., Sept., 1968.Google Scholar
3. Dembowski, P., Finite geometries, Springer-Verlag, 1968.Google Scholar
4. Dixon, J. D., The fitting subgroup of a linear solvable group, Australian Math. Soc. J. 7 (1967), 417-424.Google Scholar
5. Dixon, J. D., The maximum order of the group of a tournament, Canad. Math. Bull. 10 (1967), 503-505.Google Scholar
6. Dixon, J. D., The solvable length of a solvable linear group, Math. Z. 107 (1968), 151-158.Google Scholar
7. Feit, W. and Thompson, J. G., The solvability of groups of odd order, Pac. J. Math. 13 (1963), 775-1029.Google Scholar
8. Frucht, R., Die Gruppe des Petersenschen Graphen und des Katensysterne der regular en Polyeder, Comment. Math. Helv. 69 (1937), 217-223.Google Scholar
9. Moon, J. W., Tournaments with a given automorphism group, Can. J. Math. 16 (1964), 485-489.Google Scholar
10. Moon, J. W., Topics on Tournaments, Holt, Rinehart and Winston, 1968.Google Scholar
11. Ore, O., Theory of Graphs, A. M. S. Colloq. Pub., Providence, 1962.Google Scholar
12. Passman, D. S., P-solvable doubly transitive permutation groups, Pac. J. Math. 26 (1968). 555-577.Google Scholar
13. Passman, D. S., Permutation groups, Benjamin, 1968.Google Scholar
14. Scott, W. R., Group theory, Prentice Hall, 1964.Google Scholar
15. Wielandt, H., Finite permutation groups, Academic Press, 1964.Google Scholar