Gauss and Eisenstein Sums of Order Twelve

Abstract

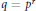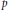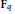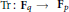Let $q\,=\,{{p}^{r}}$ with $p$ an odd prime, and ${{\mathbf{F}}_{q}}$ denote the finite field of $q$ elements. Let $\text{Tr}\,:\,{{\mathbf{F}}_{q}}\,\to \,{{\mathbf{F}}_{p}}$ be the usual trace map and set 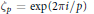${{\zeta }_{p}}\,=\,\exp (2\pi i/p)$. For any positive integer 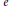$e$, define the (modified) Gauss sum 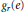${{g}_{r}}(e)$ by

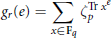$${{g}_{r}}(e)=\underset{x\in {{\mathbf{F}}_{q}}}{\mathop{\sum }}\,\zeta _{p}^{\text{Tr}{{x}^{e}}}$$

Recently, Evans gave an elegant determination of 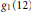${{g}_{1}}(12)$ in terms of 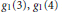${{g}_{1}}(3),\,{{g}_{1}}(4)$ and 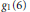${{g}_{1}}(6)$ which resolved a sign ambiguity present in a previous evaluation. Here I generalize Evans' result to give a complete determination of the sum 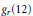${{g}_{r}}(12)$.