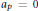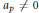Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Choi, Suh Hyun
and
Kim, Byoung Du
2017.
Congruences of two-variable p-adic L-functions of congruent modular forms of different weights.
The Ramanujan Journal,
Vol. 43,
Issue. 1,
p.
163.
Sprung, Florian
2017.
On pairs of p-adic L-functions for weight-two modular forms.
Algebra & Number Theory,
Vol. 11,
Issue. 4,
p.
885.
LEI, ANTONIO
and
PALVANNAN, BHARATHWAJ
2019.
CODIMENSION TWO CYCLES IN IWASAWA THEORY AND ELLIPTIC CURVES WITH SUPERSINGULAR REDUCTION.
Forum of Mathematics, Sigma,
Vol. 7,
Issue. ,
Lei, Antonio
and
Sprung, Florian
2020.
Ranks of elliptic curves over $$\mathbb{Z}_p^2$$-extensions.
Israel Journal of Mathematics,
Vol. 236,
Issue. 1,
p.
183.
Büyükboduk, Kâzım
and
Lei, Antonio
2021.
Iwasawa Theory of Elliptic Modular Forms Over Imaginary Quadratic Fields at Non-ordinary Primes.
International Mathematics Research Notices,
Vol. 2021,
Issue. 14,
p.
10654.
Ito Sprung, Florian
2022.
Chromatic Selmer groups and arithmetic invariants of elliptic curves.
Journal de Théorie des Nombres de Bordeaux,
Vol. 33,
Issue. 3.2,
p.
1103.
Ito Sprung, Florian
2024.
On Iwasawa main conjectures for elliptic curves at supersingular primes: Beyond the case a = 0.
Advances in Mathematics,
Vol. 449,
Issue. ,
p.
109741.
Sprung, Florian
2024.
La matrice de logarithme en termes de chiffres p-adiques.
Annales mathématiques du Québec,
Vol. 48,
Issue. 2,
p.
519.