Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T08:20:16.546Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponents of Class Groups of Quadratic Function Fields over Finite Fields

Published online by Cambridge University Press:  20 November 2018

David A. Cardon  and
M. Ram Murty
David A. Cardon
Affiliation:
Department of Mathematics Brigham Young University Provo, Utah 84602 USA, email: [email protected]
M. Ram Murty
Affiliation:
Department of Mathematics and Statistics Queen’s University Kingston, Ontario K7L 3N6, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

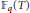We find a lower bound on the number of imaginary quadratic extensions of the function field ${{\mathbb{F}}_{q}}\left( T \right)$ whose class groups have an element of a fixed order.

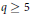More precisely, let $q\,\ge \,5$ be a power of an odd prime and let 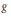$g$ be a fixed positive integer 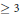$\ge \,3$. There are 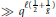$\gg \,{{q}^{\ell \left( \frac{1}{2}+\frac{1}{g} \right)}}$ polynomials 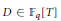$D\,\in \,{{\mathbb{F}}_{q}}\left[ T \right]$ with 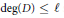$\deg \left( D \right)\,\le \,\ell $ such that the class groups of the quadratic extensions 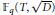${{\mathbb{F}}_{q}}\left( T,\,\sqrt{D} \right)$ have an element of order 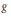$g$.

Keywords

11R5811R29class numberquadratic function field
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 4 , 01 December 2001 , pp. 398 - 407
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Artin, E., Quadratische Körper im Gebiet der höheren Kongruenzen I, II. Math. Z. 19 (1924), 153–246.Google Scholar
[2] Ankeny, N. and Chowla, S., On the divisibility of the class numbers of quadratic fields. Pacific J. Math. 5 (1955), 321–324.Google Scholar
[3] Cohen, H. and Lenstra, H. W. Jr., Heuristics on class groups of number fields. Number Theory (Noordwijkerhout, 1983) Proceedings, Springer Lecture Notes in Math. 1068, 1984.Google Scholar
[4] Davenport, H. and Heilbronn, H., On the density of discriminants of cubic fields, II. Proc. Royal Soc. London Ser. A 322 (1971), 405–420.Google Scholar
[5] Gupta, R. and Ram Murty, M., Class groups of quadratic functions fields. In preparation.Google Scholar
[6] Friedman, Eduardo and Washington, Lawrence C., On the distribution of divisor class groups of curves over finite fields. In: Théorie des nombres (Quebec, PQ 1987), de Gruyter, Berlin, 1989, 227–239.Google Scholar
[7] Friesen, Christian, Class number divisibility in real quadratic function fields. Canad. Math. Bull. (3) 35 (1992), 361–370.Google Scholar
[8] Hartung, P., Proof of the existence of infinitely many imaginary quadratic fields whose class number is not divisible by 3. J. Number Theory 6 (1974), 276–278.Google Scholar
[9] Honda, T., A few remarks on class numbers of imaginary quadratic fields. Osaka J. Math. 12 (1975), 19–21.Google Scholar
[10] Ram Murty, M., The ABC conjecture and exponents of class groups of quadratic fields. Contemp. Math. 210 (1998), 85–95.Google Scholar
[11] Ram Murty, M., Exponents of class groups of quadratic fields. Topics in Number Theory (University Park, PA, 1997), Math. Appl. 467, Kluwer Acad. Publ., Dordrecht, 1999, 229–239.Google Scholar
[12] Nagell, T., Über die Klassenzahl imaginär quadratischer Zahlkörper. Abh. Math. Sem. Univ. Hamburg, 1 (1922), 140–150.Google Scholar
[13] Weinberger, P., Real Quadratic Fields with Class Numbers Divisible by n. J. Number Theory, 5 (1973), 237–241.Google Scholar
[14] Yamamoto, Y., On unramified Galois extensions of quadratic number fields. Osaka J. Math. 7 (1970), 57–76.Google Scholar
[15] Yu, Jiu-Kang, Toward the Cohen-Lenstra conjecture in the function field case. Preprint.Google Scholar